Ángulos suplementarios: Definición, propiedades y ejemplos
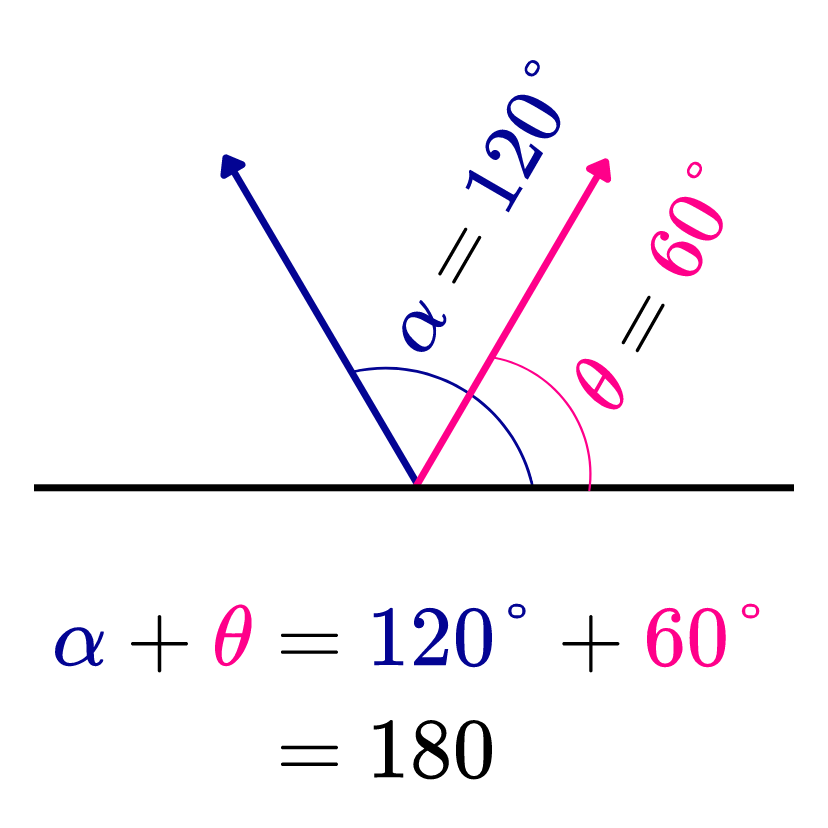
¿Qué son los ángulos suplementarios? Dos ángulos son suplementarios cuando la suma de sus medidas es igual a 180°.
Por ejemplo, si la medida de un ángulo α es de 120° y la medida de un ángulo θ es de 60°, entonces α es un ángulo suplementario del ángulo θ, ya que al sumar 120° más 60° se obtiene un ángulo de 180°.
En radianes, dos ángulos son suplementarios cuando la suma de sus medidas es igual a π radianes. Por ejemplo, si la medida de un ángulo α es de π/4 radianes y la medida de un ángulo θ es de 3π/4 radianes, entonces α es un ángulo suplementario del ángulo θ, ya que al sumar π/4 radianes más 3π/4 radianes se obtienen π radianes.
En resumen, si la suma de las medidas de dos ángulos es igual a 180°, entonces se dice que los ángulos son suplementarios.
La palabra suplementario proviene del latín supplere, que significa completar o "suplir".
Definición de ángulos suplementarios
Un ángulo α es suplementario de un ángulo θ si la suma de sus medidas es igual a 180°. Matemáticamente, α es un ángulo suplementario del ángulo θ si se cumple la siguiente igualdad:
Si esta igualdad se cumple, entonces α y θ son ángulos suplementarios entre sí.
Ejemplos de ángulos suplementarios
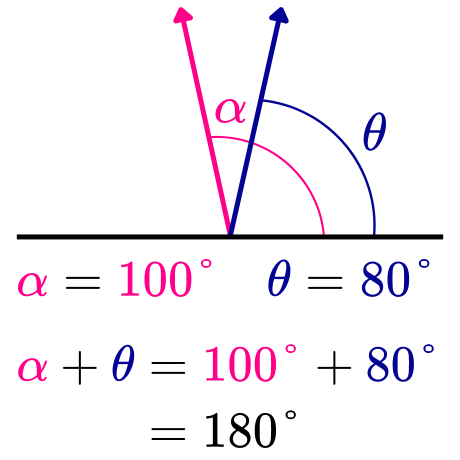
Ejemplo 1. Un ángulo α de 100° es un ángulo suplementario de un ángulo θ de 80°, ya que la suma de las medidas de estos ángulos es igual a 180°. Matemáticamente se cumple lo siguiente:
Por lo tanto, los ángulos α y θ, cuyas medidas son 100° y 80°, son ángulos suplementarios.
Ejemplo 2. Si la medida de un ángulo α es de 179°, entonces su ángulo suplementario θ debe medir 1°, ya que la suma de estos ángulos es igual a 180°. Matemáticamente, si θ es un ángulo suplementario del ángulo α, entonces se cumple que α+θ=180°.
Ejemplo 3. Si las medidas de dos ángulos α y θ son 2π/3 radianes y π/3 radianes, respectivamente, entonces α y θ son ángulos suplementarios si la suma de sus medidas es igual a π radianes.
Al sumar las medidas de los ángulos en radianes, se obtiene lo siguiente:
Por lo tanto, los ángulos α y θ, cuyas medidas son 2π/3 radianes y π/3 radianes, son ángulos suplementarios.
Cálculo de ángulos suplementarios
Dado que dos ángulos α y θ son suplementarios si la suma de sus medidas es igual a 180 grados, es decir, α y θ son ángulos suplementarios si se cumple la igualdad α+θ=180°.
Cuando se conoce el valor de uno de los ángulos, ya sea α o θ, se puede hallar el valor del ángulo suplementario despejando el ángulo desconocido de la ecuación.
Por ejemplo, para hallar el valor del ángulo suplementario de α, simplemente se despeja θ de la ecuación:
De esta manera, el ángulo θ=180°-α es el ángulo suplementario de α.
De forma similar, para hallar el valor del ángulo suplementario de θ, se despeja α de la ecuación:
De este modo, el ángulo α=180°-θ es el ángulo suplementario de θ.
En resumen, para calcular el valor del ángulo suplementario de un ángulo específico, solo es necesario restar el valor del ángulo conocido de 180°.
Ejemplo 4. Si la medida de un ángulo α es de 35°, ¿Cuál es el valor de su ángulo suplementario?
Si θ es un ángulo suplementario de α, cuya medida es de 35°, entonces la suma de sus medidas debe ser igual a 180°. Es decir, debe cumplirse la igualdad α+θ=180°
Al despejar θ de la ecuación, sustituir el valor del ángulo conocido (α=35°) y resolver la resta, se obtiene el valor del ángulo suplementario:
Por lo tanto, el valor del ángulo suplementario de α, que mide 35°, es 145°.
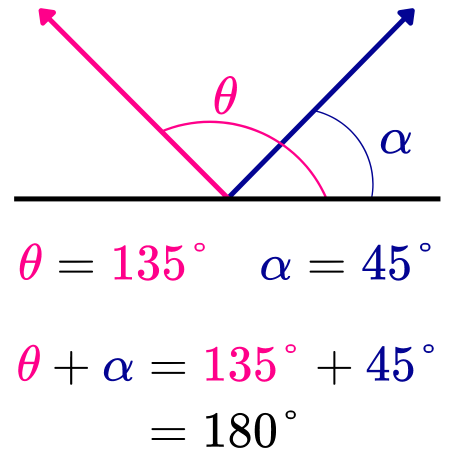
Propiedades de los ángulos suplementarios
- Dos ángulos son suplementarios si la suma de sus medidas es igual a 180°.
- Un ángulo es o tiene suplementario si mide menos de 180°. En otras palabras, para que dos ángulos sean suplementarios, ambos deben medir menos de 180°.
- El ángulo suplementario de un ángulo obtuso es un ángulo agudo.
- El ángulo suplementario de un ángulo agudo es un ángulo obtuso.
- Dos ángulos agudos (ángulos mayores que 0° y menores que 90°) no pueden ser suplementarios, ya que su suma siempre es menor que 180°.
- Dos ángulos obtusos (ángulos mayores que 90° y menores que 180°) no pueden ser suplementarios, ya que su suma siempre es mayor que 180°.
- Los ángulos suplementarios pueden ser adyacentes o no adyacentes. Es decir, pueden compartir un vértice y estar uno al lado del otro, o pueden estar completamente separados.
Diferencia entre ángulos suplementarios y ángulos complementarios
La diferencia entre ángulos suplementarios y ángulos complementarios radica en la suma de sus medidas.
Por un lado, dos ángulos son suplementarios cuando la suma de sus medidas es igual a 180 grados. Una característica importante es que cuando se suman, forman un ángulo llano (una línea recta).
Por otro lado, dos ángulos son complementarios cuando la suma de sus medidas es igual a 90 grados. Una característica importante de estos ángulos es que, al sumarse, forman un ángulo recto.
En resumen, la diferencia clave entre ángulos suplementarios y complementarios es que los ángulos suplementarios suman 180°, mientras que los ángulos complementarios suman 90°.
Tipos y clasificación de ángulos suplementarios
Los ángulos suplementarios se pueden clasificar en dos tipos principales: adyacentes y no adyacentes.
Ángulos suplementarios adyacentes
Los ángulos suplementarios adyacentes son aquellos que comparten un vértice y un lado común, es decir, se encuentran uno seguido del otro, formando juntos un ángulo llano. La siguiente imagen muestra un ejemplo de ángulos suplementarios adyacentes.
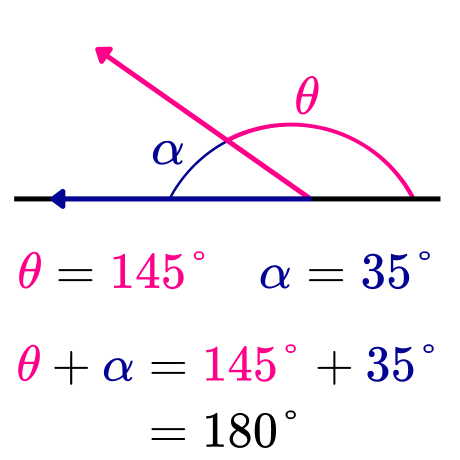
Ángulos suplementarios no adyacentes
Los ángulos suplementarios no adyacentes son aquellos que no comparten vértice ni lados. Aunque no están juntos, la suma de sus medidas sigue siendo 180°. La siguiente imagen muestra un ejemplo de ángulos suplementarios no adyacentes.
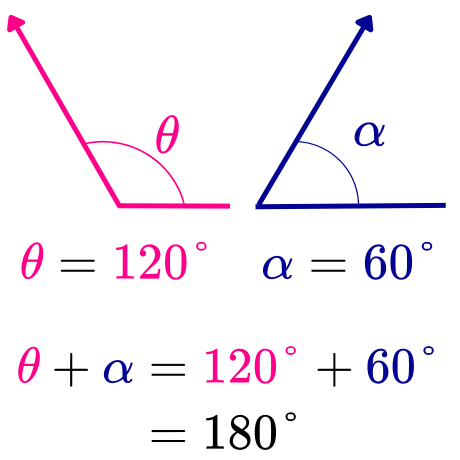
Para más información acerca del tema, puedes consultar el artículo "Ángulo suplementario: Qué es y cómo se calcula" del sitios Economipedia.