Definición de ángulo, tipos de ángulos y cómo se miden

En geometría euclidiana, un ángulo es una figura geométrica formada por dos semirrectas que comparten un punto en común.
Definición de ángulo
Un ángulo es la porción del plano comprendida entre dos semirrectas que tienen un punto en común. Las semirrectas que forman el ángulo se denominan lado inicial y lado terminal, y el punto en común se denomina vértice.
Un ángulo se representa comúnmente con letras del alfabeto griego, tales como α, β y θ.
En la siguiente imagen, el segmento de recta AE corresponde al lado inicial del ángulo α, el segmento AD al lado terminal, y el punto A es el vértice de dicho ángulo.

Representación de un ángulo
En un sistema de coordenadas cartesianas bidimensional, el vértice del ángulo coincide con el origen de coordenadas (0, 0) del plano cartesiano, el lado inicial coincide con la parte positiva del eje horizontal “x”, y el lado terminal se sitúa en algún lugar del plano dependiendo de la amplitud del ángulo.

Un ángulo puede ser positivo o negativo, según el sentido del giro del lado terminal.
Ángulos positivos y negativos
Los ángulos positivos se miden en sentido contrario al giro de las manecillas del reloj, mientras que, los negativos se miden en el sentido del giro de las manecillas del reloj. En otras palabras, un ángulo es positivo cuando el giro del lado terminal se realiza en sentido antihorario, y es negativo cuando el giro se realiza en sentido horario.

Amplitud de un ángulo
Se denomina amplitud de un ángulo a la magnitud de dicho ángulo. Las unidades de amplitud para representar la magnitud de un ángulo son el radián, el grado sexagesimal y el grado centesimal. De estas tres, las más utilizadas son el grado sexagesimal y el radián.
Cuando un ángulo se mide en grados sexagesimales, su valor oscila entre 0° y 360°. En cambio, cuando se mide en radianes, el valor oscila entre 0 radianes y 2π radianes.
¿Cómo se mide un ángulo?
Para medir la amplitud de un ángulo se utiliza un transportador.
Material necesario:
- Un transportador circular o semicircular.
- Lápiz.
- Dibujo del ángulo que se desea medir.
Paso 1: Coloca el centro del transportador en el vértice del ángulo
El transportador tiene un pequeño agujero o punto en el centro de su base recta. Coloca este punto directamente sobre el vértice del ángulo.

Paso 2: Alinea la base del transportador
Coloca la recta horizontal de la base del transportador sobre el lado inicial del ángulo que se desea medir. Asegurate de que esté bien alineado.

Paso 3: Lee la medida
Observa el lado terminal del ángulo y ubica donde intercepta con la escala del transportador. El número que señala este lado corresponde al valor de la amplitud del ángulo en grados sexagesimales.
Tipos de ángulos
Los ángulos se clasifican de acuerdo con ciertos criterios, tales como su amplitud, su relación con otros ángulos, su posición, y los que se forman cuando dos rectas paralelas son cortadas por una recta transversal.
Tipos de ángulos según su amplitud
- Ángulo nulo: Es el que mide exactamente 0°.
- Ángulo agudo: Es el aquel que mide más de 0° y menos de 90°.
- Ángulo recto: Es aquel que mide exactamente 90°.
- Ángulo obtuso: Es aquel que mide más de 90° y menos de 180°.
- Ángulo llano: Es aquel que mide exactamente 180°.
- Ángulo completo o perigonal: Es aquel que mide exactamente 360°.
La siguiente imagen muestra los tipos de ángulos según su amplitud.

Tipos de ángulos según su relación con otro ángulo
- Ángulos complementarios: Son aquellos en los que la suma de sus amplitudes es igual a 90°.
- Ángulos suplementarios: Son aquellos en los que la suma de sus amplitudes es igual a 180°.
- Ángulos conjugados: Son aquellos en los que la suma de sus amplitudes es igual a 360°.
- Ángulos congruentes: Son aquellos que tienen la misma amplitud, es decir, miden lo mismo.
La siguiente imagen muestra la clasificación de ángulos según su relación con otro ángulo.

Tipos de ángulos según su posición
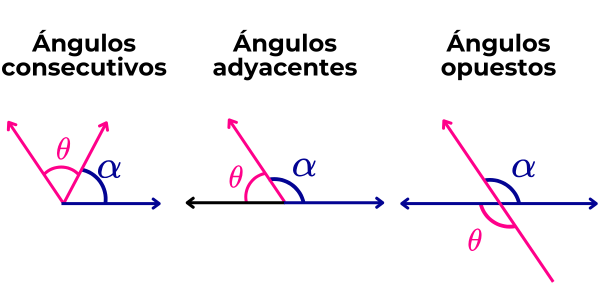
- Ángulos consecutivos: Son aquellos que comparten el vértice y uno de sus lados.
- Ángulos adyacentes. Similar a los ángulos consecutivos, los ángulos adyacentes son aquellos que comparten el vértice y uno de sus lados, además de que la suma de sus amplitudes es igual a 180°.
- Ángulos opuestos. Son aquellos que comparten ambos lados del vértice. Las rectas que lo forman se cruzan entre sí, generando un ángulo a cada lado del vértice.
Ángulos entre paralelas cortadas por una transversal
Cuando dos rectas paralelas son cortadas por una recta transversal, se forman ocho ángulos. Estos ángulos se clasifican según su posición con respecto a las rectas paralelas y a la recta transversal.
- Ángulos alternos internos: Son aquellos que se encuentran en el interior del espacio delimitado por las rectas paralelas y se ubican en lados opuestos de la recta transversal.
- Ángulos alternos externos: Son aquellos que se encuentran en el exterior del espacio delimitado por las rectas paralelas y se ubican en lados opuestos de la recta transversal.
- Ángulos correspondientes: Son aquellos que se encuentran en el mismo lado de la recta transversal, están al mismo nivel con respecto a las rectas paralelas y son congruentes, es decir, tienen la misma magnitud.
- Ángulos colaterales internos: Son aquellos que se encuentran en el interior de las rectas paralelas, están en el mismo lado de la recta transversal y son suplementarios.
- Ángulos colaterales externos: Son aquellos que se encuentran en el exterior de las rectas paralelas, están en el mismo lado de la transversal y son suplementarios
Para más información acerca del tema consulta el artículo "Ángulo" del sitio Wikipedia.