Ángulos complementarios: Definición, propiedades y ejemplos

Dos ángulos son complementarios cuando la suma de sus amplitudes es igual a 90°.

Por ejemplo, si la medida de un ángulo α es de 30° y la medida de un ángulo θ es de 60°, entonces α es un ángulo complementario del ángulo θ, ya que al sumar sus amplitudes se obtiene un ángulo de 90°.

Definición de ángulos complementarios

Un ángulo α es complementario a un ángulo θ si al sumar sus medidas se obtiene un ángulo de 90 grados (ángulo recto). Matemáticamente, α es un ángulo complementario del ángulo θ si se cumple la siguiente igualdad:

Si esta igualdad se satisface, entonces α es complementario de θ y, a su vez, θ es complementario de α, es decir, α y θ son ángulos complementarios.

Ejemplos de ángulos complementarios

Un ángulo α de 50 grados es un ángulo complementario de un ángulo θ de 40 grados, ya que la suma de sus medidas es igual a 90 grados. Matemáticamente, se cumple que:

Por lo tanto, los ángulos α y θ, cuyas medidas son 50° y 40°, son ángulos complementarios.

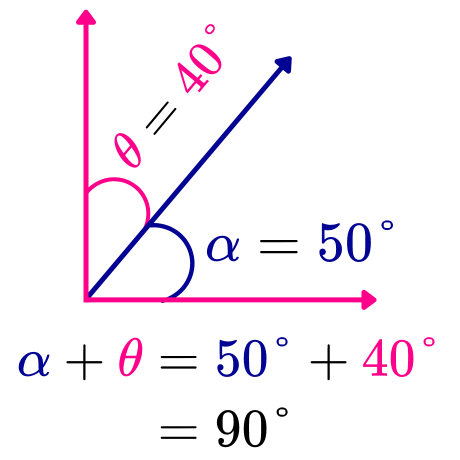
De manera similar, si la medida de un ángulo α es de 70°, entonces su ángulo complementario θ debe medir 20°, ya que la suma de las medidas de estos ángulos es igual a 90°. Matemáticamente, si θ es un ángulo complementario del ángulo α, entonces se cumple que:

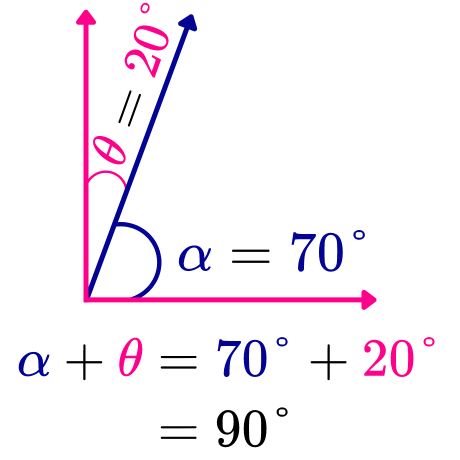
Cálculo de ángulos complementarios

Dado que dos ángulos son complementarios si la suma de sus medidas es igual a 90°, entonces un ángulo α es complementario de un ángulo θ si se cumple la siguiente igualdad:

Cuando se conoce el valor de uno de los ángulos, ya sea α o θ, puede hallarse el valor del otro despejando el ángulo desconocido de la igualdad. En otras palabras, para calcular el valor del ángulo complementario de un ángulo específico, solo es necesario restar el valor del ángulo conocido de 90°.

Por ejemplo, si la medida de un ángulo α es de 35°, entonces ¿Cuál es el valor de su ángulo complementario?

Si θ es un ángulo complementario del ángulo α, cuya medida es de 35°, entonces la suma de sus medidas debe ser igual a 90°, es decir, debe cumplirse la siguiente igualdad:

Al despejar θ de la igualdad, sustituir el valor del ángulo conocido (α=35°) y resolver la resta, se obtiene el valor del ángulo complementario:

Por lo tanto, el valor del ángulo complementario del ángulo α, que mide 35°, es igual a 55°.

Propiedades de los ángulos complementarios

• Dos ángulos son complementarios si la suma de sus medidas es igual a 90°.
• El ángulo complementario de un ángulo agudo es siempre otro ángulo agudo.
• Solo los ángulos agudos tienen ángulos complementarios. En otras palabras, para que dos ángulos sean complementarios, ambos deben ser agudos.
• Cada ángulo agudo tiene un único ángulo complementario. Es decir, si α es un ángulo agudo, entonces su ángulo complementario será igual a 90°-α.
• Si dos ángulos complementarios tienen la misma medida, entonces ambos miden 45°.
• Los ángulos complementarios pueden ser adyacentes o no adyacentes. Es decir, pueden estar uno seguido del otro o pueden estar completamente separados.
• Si α es un ángulo complementario del ángulo θ, entonces el ángulo θ también es complementario del ángulo α. En otras palabras, α y θ son ángulos complementarios entre sí
• En un triángulo rectángulo, los dos ángulos agudos siempre son complementarios, ya que la suma de los tres ángulos del triángulo es 180°, y uno de ellos es de 90°.

Tipos y clasificación de ángulos complementarios

Los ángulos complementarios se clasifican en dos tipos: adyacentes y no adyacentes.

Ángulos complementarios adyacentes

Los ángulos complementarios adyacentes son aquellos que comparten un vértice y un lado común. Es decir, se encuentran uno seguido del otro, formando un ángulo recto. La siguiente imagen muestra un ejemplo de ángulos complementarios adyacentes.

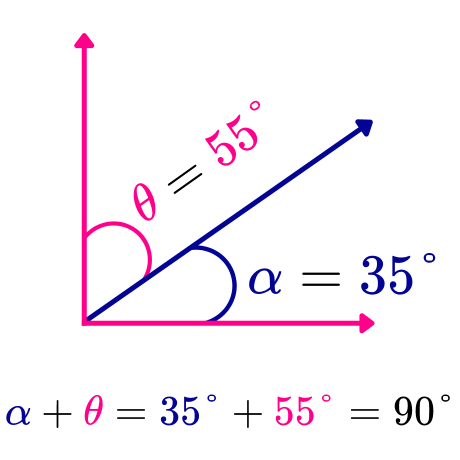
Ángulos complementarios no adyacentes

Los ángulos complementarios no adyacentes son aquellos que no comparten ni vértice ni lados. Es decir, no se encuentran uno seguido del otro, pero cumplen con la propiedad de que al sumar sus medidas se obtiene un ángulo de 90°.

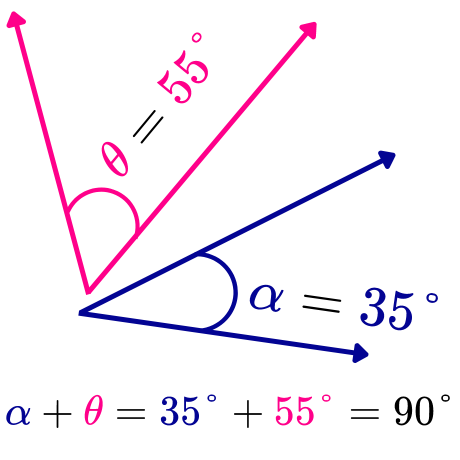
Ángulos internos de un triángulo rectángulo

En un triángulo rectángulo, dos de los ángulos internos son complementarios. Esto se debe a que un triángulo rectángulo tiene un ángulo de 90°. Dado que la suma de los ángulos internos de cualquier triángulo es de 180°, entonces si α y θ son ángulos diferentes al ángulo recto, se cumple que:

De esta ecuación, se obtiene:

Es decir, los ángulos α y θ son complementarios, ya que la suma de sus medidas es igual a 90°.

Para más información acerca del tema, puedes consultar el artículo "Ángulos complementarios. Qué son y ejemplos" del portal Smartick.