Ángulos entre paralelas cortadas por una transversal
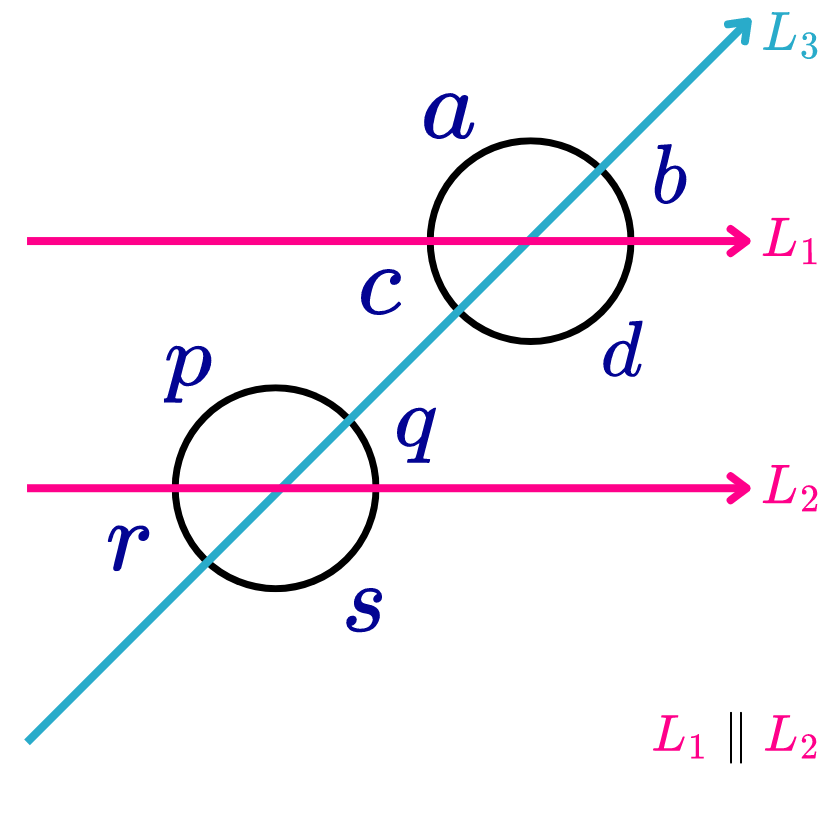
Ángulos entre paralelas cortadas por una transversal: Cuando dos rectas paralelas son cortadas por una recta transversal, se forman ocho ángulos. Estos ángulos se clasifican según su posición con respecto a las rectas paralelas y a la transversal.
Los ángulos formados por dos rectas paralelas y una transversal se agrupan en pares en las siguientes categorías:
- Ángulos alternos internos.
- Ángulos alternos externos.
- Ángulos correspondientes.
- Ángulos colaterales.
La imagen siguiente muestra dos rectas paralelas L1 y L2 cortadas por una transversal L3.
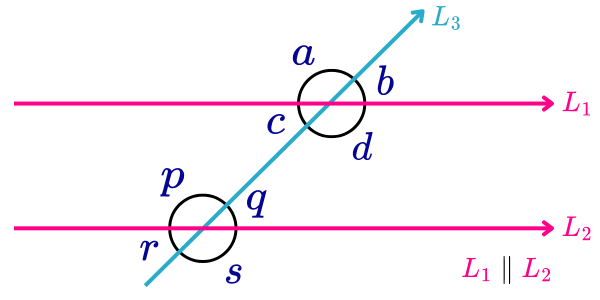
Ángulos alternos
Los ángulos alternos son aquellos que se forman cuando dos rectas paralelas son cortadas por una recta transversal. Estos ángulos se encuentran en lados opuestos de la transversal, no están al mismo nivel con respecto a las rectas paralelas y tienen la misma magnitud. Los ángulos alternos pueden ser alternos internos o alternos externos.
Ángulos alternos internos
Los ángulos alternos internos son aquellos que se forman cuando dos rectas paralelas son cortadas por una recta transversal. Estos ángulos se ubican en el interior del espacio delimitado por las rectas paralelas y se encuentran en lados opuestos de la recta transversal.
En la siguiente imagen, los ángulos internos son los ángulos c, d, p y q. De estos, los pares de ángulos alternos internos son los ángulos c y q, y d y p.
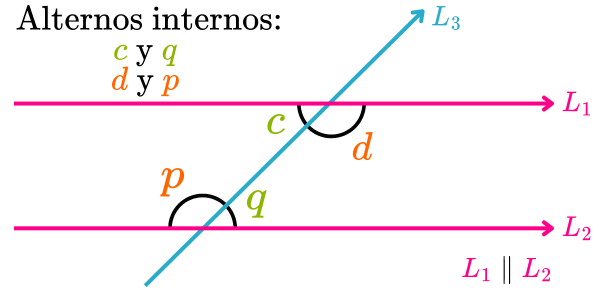
Propiedades de los ángulos alternos internos
Las propiedades de los ángulos alternos internos son las siguientes:
- Los ángulos alternos internos son congruentes, es decir, tienen la misma magnitud.
- Los ángulos internos consecutivos son ángulos suplementarios, es decir, la suma de sus medidas es igual a 180°.
- Cuando las rectas no son paralelas, los ángulos alternos internos no presentan ninguna relación geométrica específica.
Ángulos alternos externos
Los ángulos alternos externos son aquellos que se forman cuando dos rectas paralelas son cortadas por una recta transversal. Estos ángulos se encuentran en el exterior del espacio delimitado por las rectas paralelas y se ubican en lados opuestos de la recta transversal.
En la siguiente imagen, los ángulos externos son los ángulos a, b, r y s. De estos, los pares de ángulos alternos externos son los ángulos a y s, y b y r.
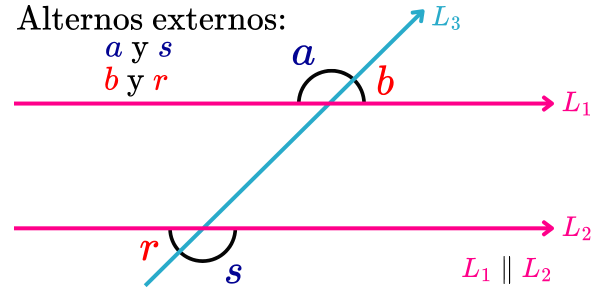
Propiedades de los ángulos alternos externos
Las propiedades de los ángulos alternos externos son las siguientes:
- Los ángulos alternos externos son congruentes, es decir, miden lo mismo.
- Los ángulos externos consecutivos son suplementarios, es decir, la suma de sus medidas es igual a 180°.
- Cuando las rectas no son paralelas, los ángulos alternos externos no presentan una relación geométrica específica.
Ángulos correspondientes
Los ángulos correspondientes son aquellos que se forman cuando dos rectas paralelas son cortadas por una recta transversal. Estos ángulos se encuentran en el mismo lado de la transversal, están al mismo nivel con respecto a las rectas paralelas y son congruentes, es decir, tienen la misma magnitud.
En la imagen siguiente, todos los pares de ángulos correspondientes son los ángulos a y p, b y q, c y r, y d y s.
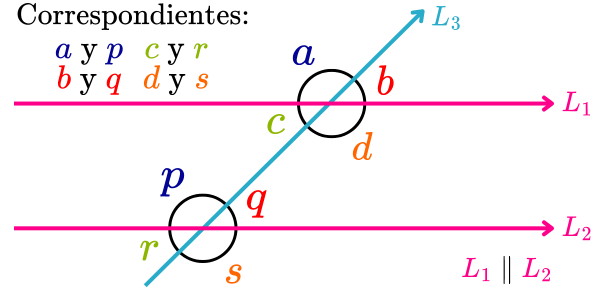
Ángulos colaterales
Los ángulos colaterales se forman cuando dos rectas paralelas son cortadas por una recta transversal. Estos ángulos pueden ser colaterales internos o colaterales externos.
Ángulos colaterales internos
Por un lado, los ángulos colaterales internos son aquellos que se encuentran en el interior de las rectas paralelas, están en el mismo lado de la recta transversal y son suplementarios, es decir, la suma de sus medidas es igual a 180°.
En la imagen siguiente, los pares de ángulos colaterales internos son los ángulos c y p, y d y q.
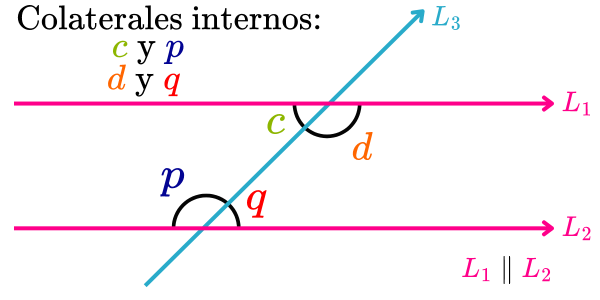
Ángulos colaterales externos
Por otro lado, los ángulos colaterales externos son aquellos que se encuentran en el exterior de las rectas paralelas, están en el mismo lado de la transversal y son suplementarios, es decir, la suma de sus medidas es igual a 180°.
En la imagen siguiente, los pares de ángulos colaterales externos son los ángulos a y r, y b y s.
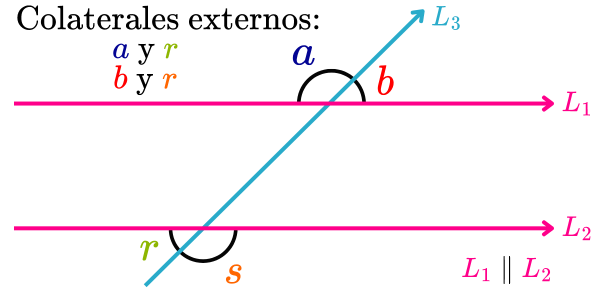
Para más información acerca del tema puedes consultar el artículo "Ángulos entre paralelas" del sitio Wikipedia.