Definición y partes de la circunferencia
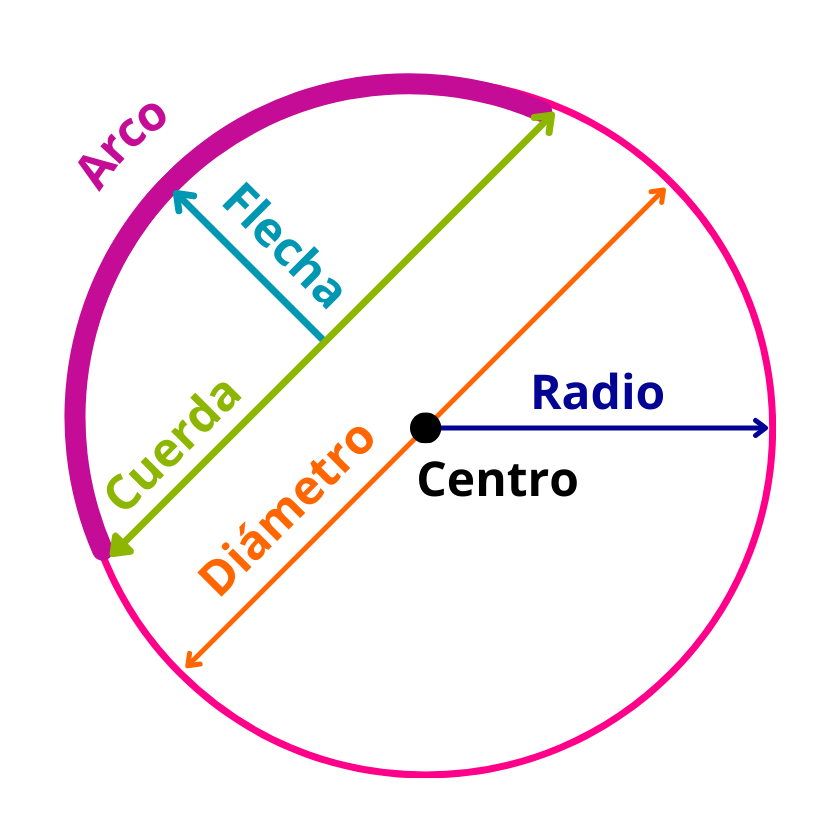
Una circunferencia es una línea curva cerrada conformada por un conjunto de puntos en un mismo plano que se encuentran a una misma distancia “r”, denominada radio, respecto de un punto fijo “c” denominado centro.
Definición de circunferencia
Una circunferencia es el lugar geométrico de todos los puntos de un plano que se encuentran a una misma distancia respecto de un punto fijo, denominado centro de la circunferencia.
La distancia que separa cada punto de la circunferencia del centro se denomina radio de la circunferencia.
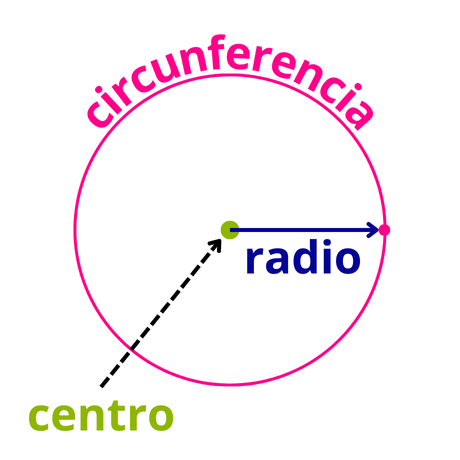
Diferencia entre círculo y circunferencia
La principal diferencia entre circunferencia y círculo es que la circunferencia es un lugar geométrico, mientras que el círculo es una región del plano.
Por un lado, una circunferencia es el lugar geométrico de todos los puntos de un plano que se encuentran a una misma distancia "r", denominada radio de la circunferencia, respecto a un punto fijo "c", denominado centro de la circunferencia.
Por otro lado, un círculo es una región del plano que incluye todos los puntos de un plano que se encuentran a una distancia menor o igual a "r", denominada radio del círculo, respecto a un punto fijo "c", denominado centro del círculo.
Elementos de la circunferencia
Los elementos o partes de una circunferencia son los siguientes:
Centro de una circunferencia
El centro de una circunferencia es un punto en el interior que se encuentra a la misma distancia de todos los puntos de la circunferencia.

Radio de una circunferencia
El radio de una circunferencia es el segmento de recta que va desde el centro hacia cualquier punto de la circunferencia. El radio se representa con la letra “r”.
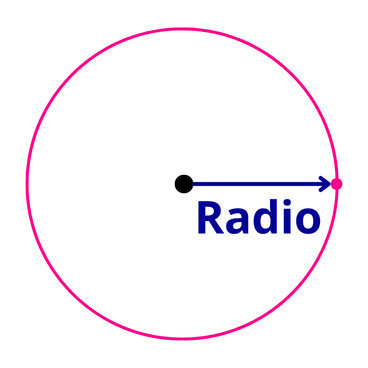
La relación entre el radio y el diámetro de una circunferencia es que la magnitud del radio es la mitad de la magnitud del diámetro. Es decir, el radio mide la mitad de la longitud del diámetro. Matemáticamente, esto se expresa de la siguiente manera:
Diámetro de una circunferencia
El diámetro de una circunferencia es el segmento de recta que toca dos puntos de la circunferencia y que pasa por el centro. El diámetro se representa con la letra “d”.
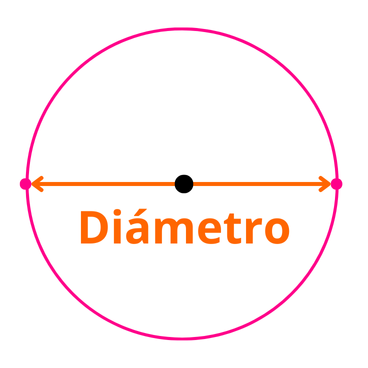
La relación entre el diámetro y el radio de una circunferencia es que la magnitud del diámetro es dos veces la magnitud del radio. Es decir, el diámetro mide dos veces la longitud del radio. Matemáticamente, esto se expresa como:
Cuerda de una circunferencia
La cuerda de una circunferencia es un segmento de recta que une dos puntos de la circunferencia sin pasar por el centro. La cuerda se representa con la letra "c" minúscula.

Dado que el diámetro de una circunferencia es el segmento de recta que une dos puntos y que pasa por el centro, entonces el diámetro es el segmento de recta de mayor magnitud que puede trazarse dentro de una circunferencia, por lo tanto, el diámetro también se considera como una cuerda de máxima longitud de una circunferencia.
Flecha o sagita de una circunferencia
La flecha o sagita de una circunferencia es el segmento de recta perpendicular a una cuerda, que va desde el punto medio de la cuerda hacía cualquier punto de la circunferencia, sin pasar por el centro. La flecha se representa con la letra "f" minúscula.
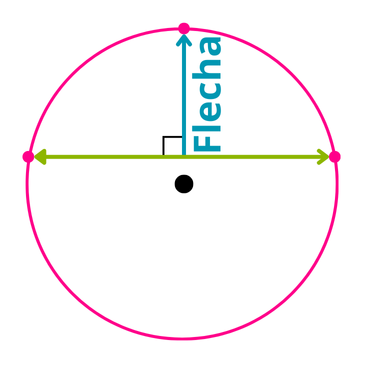
Como el diámetro es también una cuerda (la de mayor longitud), el diámetro tiene dos flechas o sagitas, las cuales corresponden a dos radios de la circunferencia.
Arco de una circunferencia
El arco de una circunferencia es una parte de la circunferencia. Un arco se forma a partir de una cuerda o del diámetro, de tal manera que un arco es cada una de las partes en las que una cuerda divide la circunferencia.
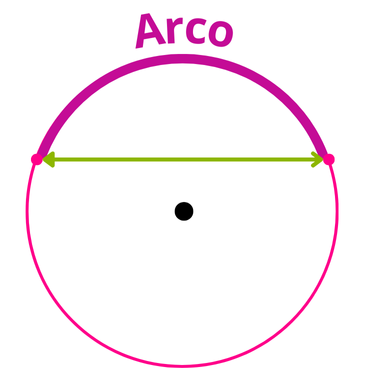
Cuando se traza una cuerda, siempre se forman dos arcos: uno de mayor longitud y otro de menor longitud. Si no se especifica, se considera arco principal al de menor tamaño. El arco de una circunferencia se denota con la letra "L".
Longitud de una circunferencia
La longitud de una circunferencia es π veces el valor de su diámetro. En otras palabras, la longitud de una circunferencia es, aproximadamente, 3.1416 veces el valor de su diámetro.
Cuando se divide la longitud de una circunferencia entre la longitud de su diámetro, el resultado es siempre la cantidad aproximada 3.14159265, que redondeando es igual a 3.1416. Este valor corresponde al número irracional pi π. Matemáticamente, esta relación se expresa de la siguiente manera:
A partir de esta relación, se puede calcular fácilmente tanto la longitud de una circunferencia (perímetro) como la longitud de su diámetro.
Perímetro
Dada una circunferencia, el perímetro es la longitud de la circunferencia.
La longitud de una circunferencia en función de su diámetro es igual a π por el valor del diámetro.
La fórmula para calcular la longitud de una circunferencia (perímetro) en función de su diámetro se expresa de la siguiente manera:
Por otra parte, la longitud de una circunferencia en función de su radio es igual a dos π por el valor de su radio.
La fórmula para calcular la longitud de una circunferencia en función de su radio está definida de la siguiente manera:
Ejemplo 1: Determinar la longitud de una rueda de 10 centímetros de diámetro.
Solución: La longitud de una rueda corresponde a la longitud de una circunferencia, es decir, al cálculo de su perímetro. Dado que se conoce la longitud del diámetro de la circunferencia, se puede hallar la longitud de la circunferencia utilizando la siguiente fórmula:
Sustituyendo el valor del diámetro en la fórmula anterior, se obtiene lo siguiente:
Por lo tanto, la longitud de una rueda de 10 centímetros de diámetro es de aproximadamente 31.4159 centímetros.
Para más información acerca del tema, puedes consultar el artículo "Circunferencia" del portal Wikipedia.