Derivada de una potencia

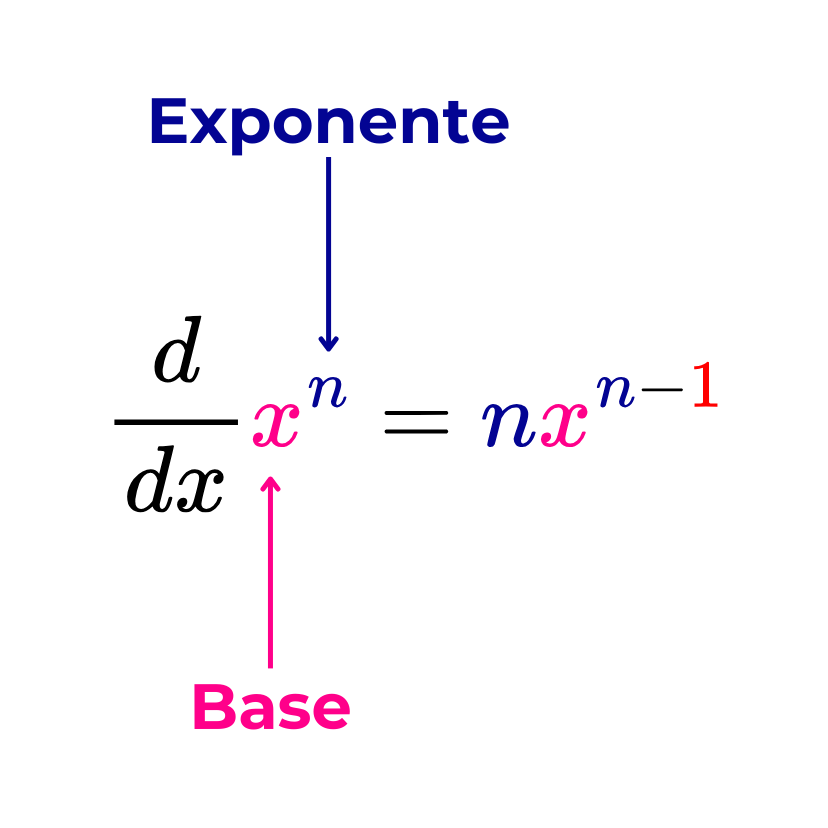
Si la base de la potencia es la función identidad g(x)=x, entonces la derivada es igual al producto del exponente por la misma base elevada al exponente reducido en una unidad. Matemáticamente, esto se expresa de la siguiente manera:

\[\frac{d}{dx}x^n=n\cdot x^{n-1}\]

Si la base de la potencia es cualquier otra función h(x), entonces la derivada es igual al producto del exponente por la misma base elevada al exponente reducido en una unidad, multiplicada por la derivada de la base. Matemáticamente, esto se expresa de la siguiente manera:

\[\frac{d}{dx}h(x)^n=n\cdot h(x)^{n-1}\cdot h’(x)\]

Tabla de contenido

Derivada de una potencia de base x
Derivada de una potencia de base g(x)

Derivada de una potencia de base x

La derivada de una potencia de base x es igual al producto del exponente por la misma base x elevada al exponente reducido en una unidad. Matemáticamente, esto se expresa de la siguiente manera:

\[\frac{d}{dx}x^n=n\cdot x^{n-1}\]

Por ejemplo, si f(x) es una función definida como f(x)=x⁴, entonces su derivada es igual al producto del exponente (4) por la base x elevada al exponente reducido en una unidad (4-1=3). Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}x^4&=4\cdot x^{4-1}\\&=4\cdot x^3\end{aligned}\]

De manera similar, para una función f(x) definida como f(x)=x^-3, su derivada es igual al producto del exponente, en este caso -3, por la base x elevada al exponente reducido en una unidad, es decir, -3-1=-4. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}x^{-3}&=-3\cdot x^{-3-1}\\&=-3\cdot x^{-4}\end{aligned}\]

Derivada de una potencia de base g(x)

Si la base de la potencia es cualquier otra función f(x) definida como f(x)=[g(x)]ⁿ, donde g(x) es una función diferenciable y n es un número real, la derivada es igual al producto del exponente n por la misma base g(x) elevada al exponente reducido en una unidad, multiplicada por la derivada de la base g'(x). Matemáticamente, esto se expresa de la siguiente manera:

\[\frac{d}{dx}g(x)^n=n\cdot g(x)^{n-1}\cdot g’(x)\]

Por ejemplo, si f(x) es una función definida como f(x)=(x⁴+2)⁶, entonces su derivada es igual al producto del exponente 6 por la base (x⁴+2) elevada al exponente reducido en una unidad (6-1=5), multiplicada por la derivada de la base g'(x)=4x³. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}(x^4+2)^6&=6\cdot (x^4+2)^{6-1}\cdot 4x^3\\&=6\cdot (x^4+2)^5\cdot 4x^3\\&=24x^3\cdot (x^4+2)^5\end{aligned}\]

De manera similar, si f(x) es una función definida como f(x)=cos²(x) (coseno cuadrado de x), entonces su derivada es igual al producto del exponente 2 por la base cos(x) elevada al exponente reducido en una unidad (2-1=1), multiplicada por la derivada de la base g(x)=cos(x): g'(x)=-sen(x). Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}\cos^2(x)&=2\cos(x)^{2-1}\cdot [-\sin(x)]\\&=-2\cdot\cos(x)\cdot\sin(x)\end{aligned}\]