Derivada del seno

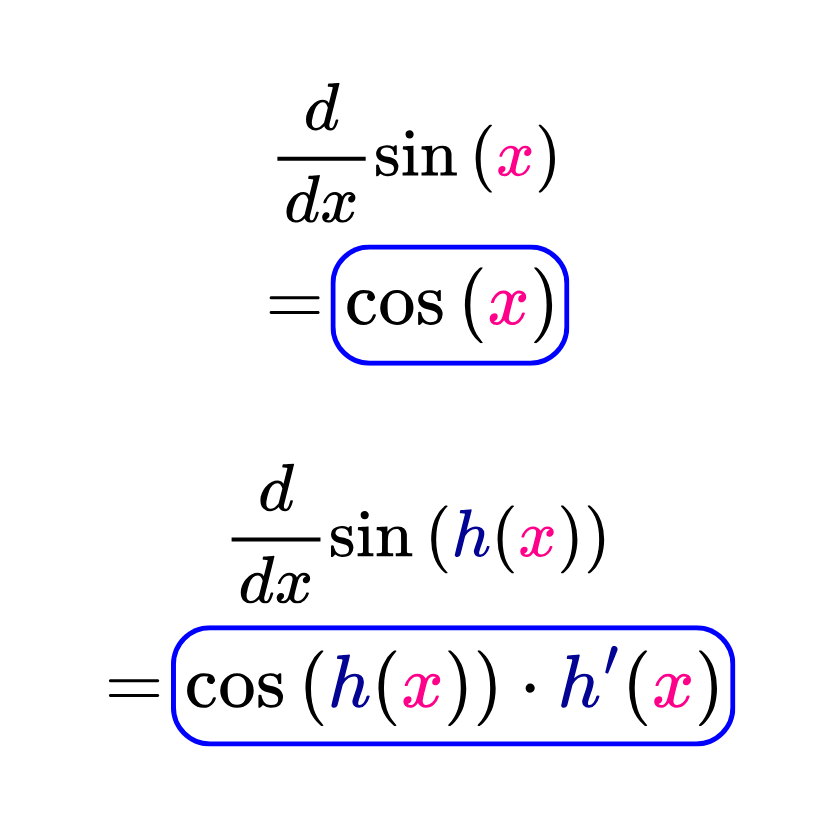
Si el argumento de la función seno es la función identidad f(x)=x, es decir, si se tiene simplemente que g(x)=sen(x), entonces su derivada es igual al coseno de x. Matemáticamente, esto se expresa como g'(x)=cos(x).

Si el argumento de la función seno es otra función h(x), es decir, si se tiene que f(x)=sen(h(x)), entonces su derivada es igual al producto de la derivada del seno, que es el coseno, cuyo argumento es la función h(x), por la derivada del argumento h(x). Matemáticamente, esto se expresa como f'(x)=cos[h(x)]∙h'(x).

Tabla de contenido

Fórmula de la derivada del seno de x
Fórmula de la derivada del seno de una función
Ejemplos
Ejercicios resueltos
Preguntas frecuentes

Fórmula de la derivada del seno de x

La derivada del seno de x con respecto a x es igual al coseno de x. Esto equivale a la derivada del seno de la función identidad f(x)=x. Es decir, si g(x)=sen(x), entonces su derivada con respecto a x es igual al coseno de x. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}g(x)&=\frac{d}{dx}\sin(x)\\&=\cos(x)\end{aligned}\]

Fórmula de la derivada del seno de una función

Cuando el argumento de la función seno es otra función h(x), es decir, cuando se tiene que f(x)=sen(h(x)), su derivada se obtiene aplicando la regla de la cadena. En este caso, la derivada de sen(h(x)) con respecto a x es igual a la derivada de la función seno, que es el coseno evaluado en h(x), multiplicado por la derivada de la función que aparece en el argumento del seno. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}f(x)&=\frac{d}{dx}\sin{\left(h(x)\right)}\\&=\cos{\left(h(x)\right)}\cdot h’(x)\end{aligned}\]

Esto significa que, en primer lugar, se deriva la función seno como si su argumento fuera simplemente x. Luego, se evalúa la función interna h(x) dentro de la derivada del seno y, por último, el resultado se multiplica por la derivada de la función h(x).

Ejemplos

Ejemplo 1. Sea la función f(x)=sen(x³). En este caso, el argumento de la función seno es la función h(x) = x³, por lo que f(x) puede reescribirse como f(x)=sen(h(x)). Para hallar su derivada, se aplica la regla de la cadena. Primero, se deriva la función seno como si su argumento fuera simplemente x, lo que da como resultado cos(x). Luego, se evalúa la función interna h(x)=x³ dentro de la derivada del seno, obteniendo cos(x³). Finalmente, este resultado se multiplica por la derivada de la función interna, que es h’(x)=3x².

Matemáticamente, se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}f(x)&=\frac{d}{dx}\sin(x^3)\\&=\cos(x^3)\cdot 3x^2\\&=3x^2\cos(x^3)\end{aligned}\]

Por lo tanto, la derivada de f(x)=sen(x³) es f’(x)=3x²cos(x³).

Ejemplo 2. Sea la función f(x)=sen(√x). En este caso, el argumento de la función seno es h(x)=√x, por lo que f(x) puede reescribirse como f(x)=sen(h(x)). Para hallar su derivada, se emplea nuevamente la regla de la cadena. Primero, se deriva la función seno como si su argumento fuera simplemente x, obteniendo cos(x). Luego, se evalúa la función interna h(x)=√x dentro de la derivada del seno, obteniendo: cos(√x). Finalmente, este resultado se multiplica por la derivada de h(x)=√x, que es h’(x)=1/(2√x).

Matemáticamente, este procedimiento se expresa de la siguiente manera:

\[\begin{aligned}\frac{d}{dx}f(x)&=\frac{d}{dx}\sin\left(\sqrt{x}\right)\\&=\cos\left(\sqrt{x}\right)\cdot \frac{1}{2\sqrt{x}}\\&=\frac{\cos(x)}{2\sqrt{x}}\end{aligned}\]

Por lo tanto, la derivada de f(x)=sen(√x) es f’(x)=cos(√x)/(2√x).

Ejercicios resueltos

Ejercicio resuelto 1. Sea la función f(x)=sen(x²+2x). En este caso, el argumento de la función seno es la función h(x)=x²+2x, por lo que f(x) puede reescribirse como f(x)=sen(h(x)). Para hallar su derivada, se aplica la regla de la cadena.

Paso 1. Se deriva la función seno como si su argumento fuera simplemente x, lo que da como resultado cos(x).
Paso 2. Se evalúa la función interna h(x)=x²+2x dentro de la derivada del seno, obteniendo así cos(x²+2x).
Paso 3. Se multiplica el resultado anterior por la derivada de la función interna, que es h’(x)=2x+2.

\[\begin{aligned}\frac{d}{dx}f(x)&=\frac{d}{dx}\sin(x^2+2x)\\&=\cos(x^2+2x)\cdot (2x+2)\\&=2x\cos(x^2+2x)+2\cos(x^2+2x)\end{aligned}\]

Por lo tanto, la derivada de f(x)=sen(x²+2x) es f’(x)=(2x+2)cos(x²+2x).

Preguntas frecuentes

¿Cuál es la derivada del seno de una función?

La derivada del seno de una función h(x) , es decir, la derivada de f(x)=sen(h(x)) es igual al coseno de la misma función h(x), multiplicado por la derivada de la función interna h(x). Matemáticamente, se expresa como d/dx sen(x)=cos(h(x))*h’(x).

¿Cuál es la derivada del seno?

La derivada de la función seno, sen(x), con respecto a x es igual a la función coseno. Matemáticamente, esto se expresa como: d/dx sen(x)=cos(x).