Dicciomat

Dirección de un vector

dirección de un vector

La dirección de un vector en el plano se define como la amplitud del ángulo que forma la recta que lo contiene con la parte positiva del eje horizontal "x" del plano cartesiano.

Tabla de contenido

Dirección de un vector en dos dimensiones

La dirección de un vector A en dos dimensiones, definido como A=(ax, ay), corresponde a la amplitud del ángulo que forma la recta que lo contiene con la parte positiva del eje horizontal "x".

Dicha amplitud se mide en sentido antihorario a partir del eje positivo "x" y su valor varía entre 0° y 360°.

¿Cómo calcular la dirección de un vector?

Para determinar la dirección de un vector en dos dimensiones, es necesario conocer sus componentes horizontal y vertical.

Sea A un vector definido como A=(ax, ay), donde “ax” es la componente horizontal y “ay” la componente vertical.

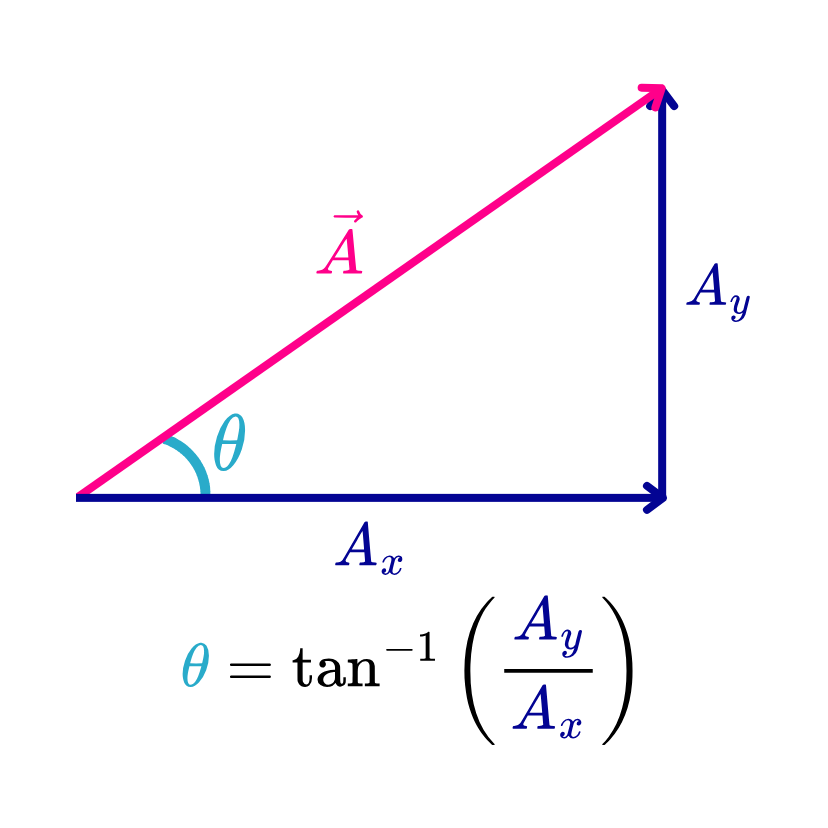
La siguiente imagen muestra una representación gráfica de un vector en el plano cartesiano. La amplitud del ángulo θ indica la dirección del vector.

Se observa que el vector forma un triángulo rectángulo, en el que las longitudes de los catetos corresponden a sus componentes “ax” (horizontal) y “ay” (vertical).

La tangente del ángulo θ se define como el cociente entre la componente vertical “ay” y la componente horizontal “ax” (cateto opuesto entre cateto adyacente). Matemáticamente, esto se expresa de la siguiente manera:

\[\tan{\theta}=\frac{a_y}{a_x}\]

Para calcular la amplitud del ángulo θ, se aplica la función tangente inversa en ambos miembros de la ecuación:

\[\tan^{-1}\left(\tan{\theta}\right)=\tan^{-1}\left(\frac{a_y}{a_x}\right)\]

De esta manera se obtiene que la amplitud del ángulo θ que forma un vector con la parte positiva del eje horizontal “x” es igual a la tangente inversa de la componente vertical ay entre la componente horizontal ax del vector. Matemáticamente, esto se expresa de la siguiente manera:

\[\theta=\tan^{-1}\left(\frac{a_y}{a_x}\right)\]

Es importante señalar que la función tangente inversa (tan⁻¹ o arctan) devuelve valores en el intervalo (-90°, 90°), lo que puede generar ambigüedades en la determinación del ángulo real. Para obtener correctamente la dirección del vector, es necesario considerar el cuadrante en el que se encuentra:

  • Primer cuadrante (ax>0, ay>0): El ángulo θ obtenido es el correcto.
  • Segundo cuadrante (ax<0, ay>0): Se suma 180° al ángulo obtenido.
  • Tercer cuadrante (ax<0, ay<0): Se suma 180° al ángulo obtenido.
  • Cuarto cuadrante (ax>0, ay<0): Se suma 360° al ángulo obtenido si es negativo.

De esta manera, se garantiza que el ángulo θ se encuentra dentro del intervalo [0°, 360°], representando correctamente la dirección del vector en el plano cartesiano.

Ejemplos

Ejemplo 1. Para determinar la dirección de un vector A definido como A=(3, 4), se debe calcular la tangente inversa del cociente entre la componente vertical ay y la componente horizontal ax.

En este caso, la componente horizontal es ax=3 y la componente vertical es ay=4, por lo que la amplitud del ángulo θ se determina de la siguiente manera:

\[\begin{aligned}\theta&=\tan^{-1}\left(\frac{a_y}{a_x}\right)\\&=\tan^{-1}\left(\frac{4}{3}\right)\end{aligned}\]

Al realizar el cálculo en una calculadora, se obtiene que la amplitud del ángulo θ es aproximadamente 53.1°.

Dado que el vector se encuentra en el primer cuadrante, el valor obtenido es correcto. Por lo tanto, la dirección de este vector A es de 53.1° con respecto a la parte positiva del eje horizontal "x".

Ejemplo 2. Dado un vector B en dos dimensiones definido como B=(-3, 4), para determinar su dirección se calcula la tangente inversa del cociente entre la componente vertical ay y la componente horizontal ax.

En este caso, la componente horizontal es ax=-3 y la componente vertical es ay=4, por lo que la amplitud del ángulo θ se determina de la siguiente manera:

\[\begin{aligned}\theta&=\tan^{-1}\left(\frac{a_y}{a_x}\right)\\&=\tan^{-1}\left(\frac{-4}{3}\right)\\&=\tan^{-1}\left(-\frac{4}{3}\right)\end{aligned}\]

Al realizar el cálculo en una calculadora, se obtiene que la amplitud del ángulo θ es aproximadamente -53.1°.

Este valor representa un ángulo medido con respecto al eje positivo "x", pero en sentido horario. Sin embargo, como el vector se encuentra en el segundo cuadrante, se debe sumar 180° para obtener el ángulo correcto. Al realizar la suma se obtiene lo siguiente:

\[\begin{aligned}\theta&=-53.1°+180°\\&=126.9°\end{aligned}\]

Por lo tanto, la dirección de este vector B es de 126.9° con respecto a la parte positiva del eje horizontal "x".

Preguntas frecuentes

¿Qué es la dirección de un vector?

La dirección de un vector en dos dimensiones es la amplitud del ángulo que forma con la parte positiva del eje horizontal "x" en un sistema de coordenadas cartesianas. Se mide en grados o radianes y en sentido antihorario desde el eje positivo "x".

¿Cómo se calcula la dirección de un vector?

Para calcular la dirección de un vector, primero se identifican los valores numéricos de sus componentes horizontal y vertical. Luego, se calcula la tangente inversa del cociente entre la componente vertical ay y la componente horizontal ax del vector: θ=tan⁻¹(ay/ax). Es importante considerar el cuadrante en el que se encuentra el vector para determinar correctamente el ángulo dentro del intervalo de 0° a 360°.