Distancia entre dos puntos fórmula y ejemplos
La distancia entre dos puntos es la longitud del segmento de recta que los une.
En el plano cartesiano, la distancia entre dos puntos A y B, con coordenadas (x1, y1) y (x2, y2), respectivamente, se representa como d(A, B) y se calcula mediante la fórmula d(A, B)=√((x2-x1)2+(y2-y1)2).
Fórmula para calcular la distancia entre dos puntos
La fórmula para calcular la distancia entre dos puntos A y B, con coordenadas (x1, y1) y (x2, y2), respectivamente, está definida de la siguiente manera:
Esta fórmula establece que la distancia entre dos puntos en el plano cartesiano es igual a la raíz cuadrada de la suma de los cuadrados de las diferencias entre sus coordenadas correspondientes.
Deducción de la fórmula para calcular la distancia entre dos puntos
La deducción de la fórmula para calcular la distancia entre dos puntos se basa en el teorema de Pitágoras y en las coordenadas de dichos puntos en el plano cartesiano.
Para deducir la fórmula, sean A y B dos puntos en el plano cartesiano, cuyas coordenadas son (x1, y1) y (x2, y2), respectivamente.
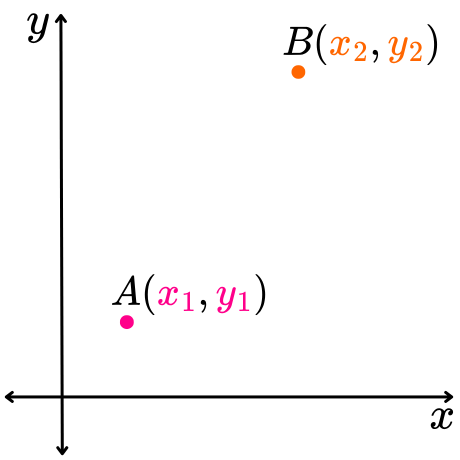
La distancia entre estos dos puntos se denota como d(A,B) y corresponde a la longitud del segmento de recta que va desde el punto A hacía el punto B.
Para hallar la longitud de este segmento de recta, primero se traza una línea recta paralela al eje horizontal “x”, cuya longitud es x2-x1 (diferencia de abscisas). Luego, se traza una línea recta paralela al eje vertical “y”, cuya longitud es y2-y1 (diferencia de ordenadas).
Al trazar estas líneas, se forma un triángulo rectángulo, donde la hipotenusa es la distancia entre los puntos A y B.
El teorema de Pitágoras establece que, en un triángulo rectángulo, la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa. Matemáticamente, esto se expresa de la siguiente manera:
Al aplicar el teorema de Pitágoras al triángulo formado, se obtiene la siguiente expresión:
Para obtener d(A, B), se calcula la raíz cuadrada en ambos miembros de la igualdad:
De donde se obtiene que:
Por lo tanto, la fórmula para calcular la distancia entre dos puntos queda definida de la siguiente manera:
Distancia entre dos puntos oblicua
La distancia oblicua se refiere al caso en el que los puntos no están alineados ni en una misma línea horizontal ni vertical, sino en una dirección inclinada.
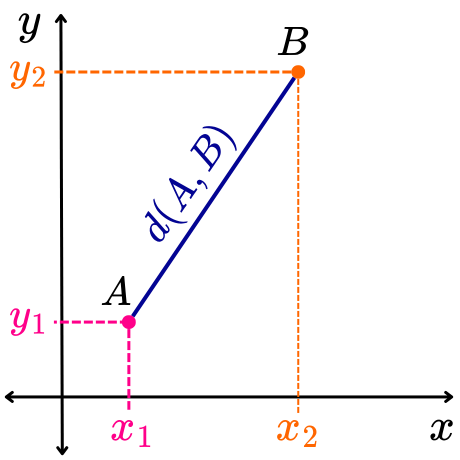
La fórmula para calcular la distancia entre dos puntos A y B que se encuentran sobre una misma recta oblicua (recta inclinada) está definida de la siguiente manera:
Distancia entre dos puntos alineados horizontalmente
La fórmula para calcular la distancia entre dos puntos A y B que se encuentran sobre una misma recta horizontal está definida de la siguiente manera:
Dos puntos a y b se encuentran sobre una misma recta horizontal cuando el valor de sus coordenadas verticales es el mismo. Es decir, dos puntos A y B, con coordenadas (x1, y1) y (x2, y2), respectivamente, se encuentran sobre una misma recta horizontal si y1=y2.
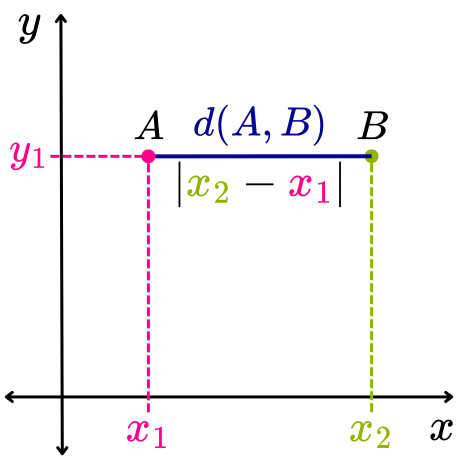
De tal manera que, cuando dos puntos A y B están alineados horizontalmente, sus coordenadas son (x1, y1) y (x2, y1), respectivamente. Al aplicar la fórmula para calcular la distancia entre los puntos A y B, se obtiene lo siguiente:
Así, la distancia entre dos puntos alineados horizontalmente es igual al valor absoluto de la diferencia de sus abscisas.
Distancia entre dos puntos alineados verticalmente
La fórmula para calcular la distancia entre dos puntos A y B que se encuentran sobre una misma recta vertical está definida de la siguiente manera:
Dos puntos A y b se encuentran sobre una misma recta vertical cuando el valor de sus coordenadas horizontales es la misma. Es decir, dos puntos A y B, con coordenadas (x1, y1) y (x2, y2), respectivamente, se encuentran sobre una misma recta vertical si x1=x2.
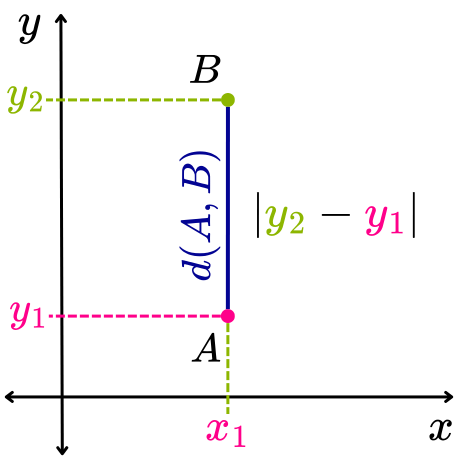
De tal manera que, cuando dos puntos A y B están alineados verticalmente, sus coordenadas son (x1, y1) y (x1, y2), respectivamente.
Al aplicar la fórmula para calcular la distancia entre los puntos a y b, se obtiene lo siguiente:
Por lo tanto, la distancia entre dos puntos alineados verticalmente es igual al valor absoluto de la diferencia de sus ordenadas.
Distancia entre dos puntos ejemplos
Ejemplo 1. Calcular la distancia entre los puntos A y B cuyas coordenadas cartesianas son (-6, 3) y (2, -3), respectivamente.
Solución: la distancia entre dos puntos A y B es igual a la longitud del segmento de recta que va desde el punto A hacia el punto B. La fórmula para calcular la distancia entre dos puntos está definida como:
En esta fórmula, (x1, y1) corresponde a las coordenadas del punto A y (x2, y2) a las coordenadas del punto B.
Dado que las coordenadas del punto A son (-6, 3), se tiene que x1=-6 y y1=3. Además, como las coordenadas del punto B son (2, -3), se tiene que x2=2 y y2=-3.
Al sustituir estos valores en la fórmula para calcular la distancia entre dos puntos, obtenemos lo siguiente:
Por lo tanto, la distancia entre los puntos A y B, cuyas coordenadas son (-6, 3) y (2, -3), respectivamente, es igual a 10 unidades de longitud.
Para más información acerca del tema, consulta el artículo "Cálculo de la distancia entre dos puntos" del sitio Superprof.