Circunferencia con centro en el origen

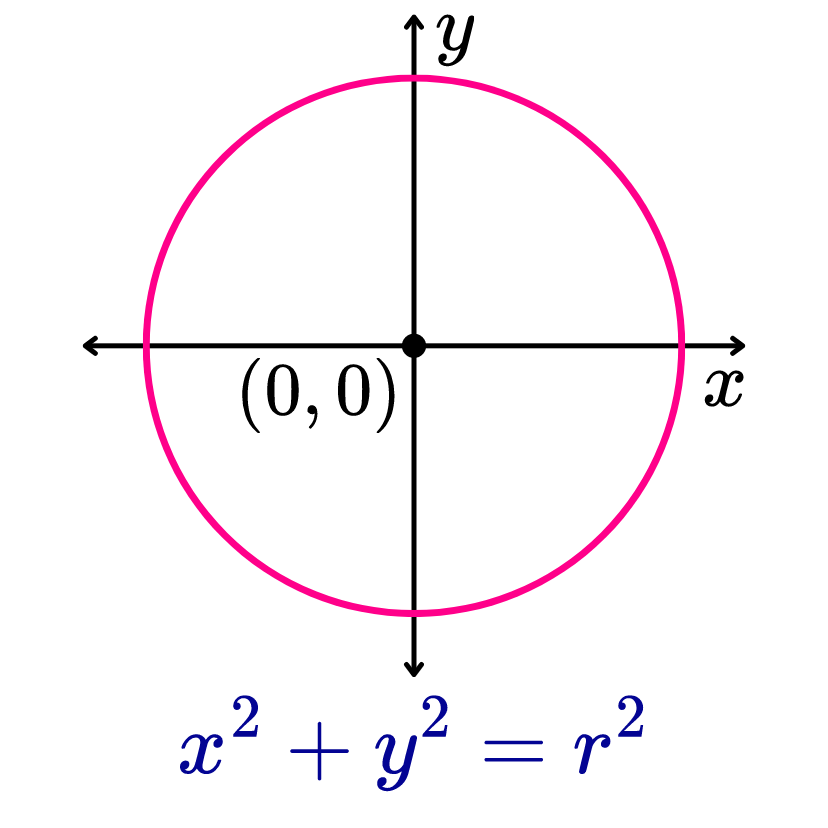
Una circunferencia con centro en el origen es aquella cuya centro se encuentra en el origen de coordenadas (0, 0) del plano cartesiano.

Es necesario destacar que una circunferencia es el lugar geométrico de todos los puntos de un plano que se encuentran a una misma distancia "r", denominada radio de la circunferencia, respecto a un punto fijo "C", denominado centro de la circunferencia.

Ecuación de la circunferencia con centro en el origen

La ecuación de la circunferencia con centro en el origen (0,0) está definida como x²+y²=r².

En esta ecuación, “x” y “y” representan las coordenadas (x, y) de cualquier punto de la circunferencia, y “r” representa el radio de la circunferencia.

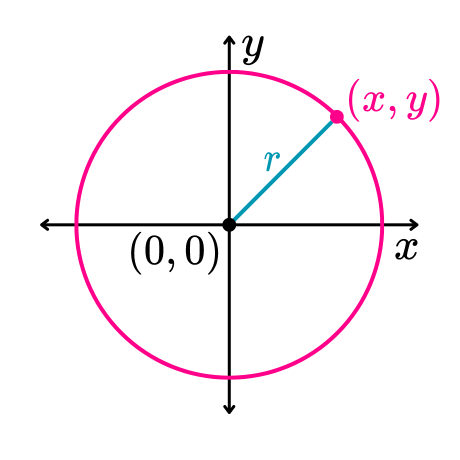
Cómo hallar la ecuación de la circunferencia con centro en el origen

Para hallar la ecuación de una circunferencia con centro en el origen es necesario conocer el valor del radio de la circunferencia.

Dado que “r” representa el radio de la circunferencia, al sustituir el valor del radio en la ecuación x²+y²=r², se obtiene la ecuación de la circunferencia con centro en el origen.

Ejemplos

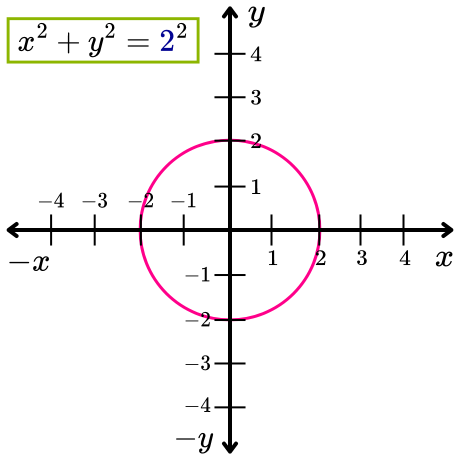
Ejemplo 1. Encuentra la ecuación de la circunferencia con centro en el origen de radio 2.

Solución. Como el radio de la circunferencia es r=2, entonces al sustituir este valor en la ecuación de la circunferencia con centro en el origen x²+y²=r², se obtiene lo siguiente:

Al desarrollar la potencia, se obtiene lo siguiente:

Por lo tanto, la ecuación de una circunferencia con centro en el origen y radio 2 está definida como x²+y²= 4.

La siguiente imagen muestra una circunferencia con centro en el origen de radio 2.

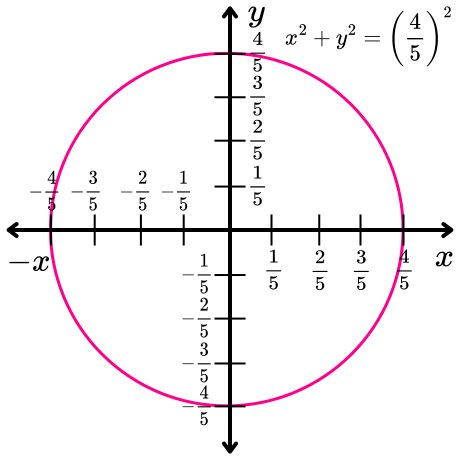
Ejemplo 2. Determina la ecuación de la circunferencia con centro en el origen y radio r=4/5.

Solución. La ecuación de la circunferencia con centro en el origen está definida como x²+y²=r². Dado que el radio de la circunferencia es r=4/5, entonces al sustituir este valor en la ecuación y desarrollar la potencia, se obtiene lo siguiente:

De esta manera, se obtiene que la ecuación de una circunferencia con centro en el origen y radio r=4/5 está definida como x²+y²=16/25.

La siguiente imagen muestra una circunferencia con centro en el origen y radio igual a 4/5.

Ejercicios resueltos

Ejercicio resuelto 1. Encuentra la ecuación de la circunferencia con centro en el origen de una circunferencia de radio r=√5.

Solución: Como se conoce el valor del radio de la circunferencia, entonces al sustituir este valor en la ecuación de la circunferencia con centro en el origen definida como x²+y²=r², se obtiene lo siguiente:

Al desarrollar la potencia aplicando las leyes de los exponentes, se obtiene lo siguiente:

Por lo tanto, la ecuación de la circunferencia con centro en el origen de una circunferencia de radio r=√5 es x²+y²=5.

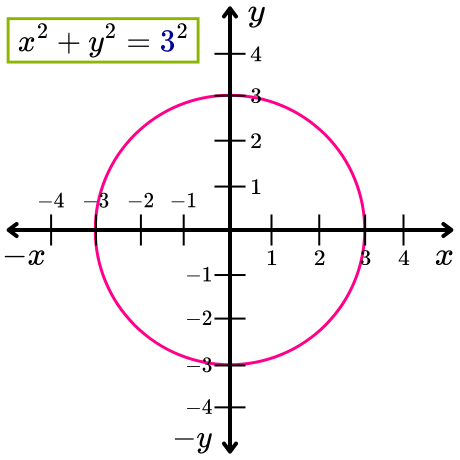
Ejercicio resuelto 2. Determina el radio de la circunferencia definida por la ecuación x²+y²=9.

Solución: Dado que la ecuación de la circunferencia con centro en el origen está definida como x²+y²=r², entonces al comparar esta ecuación con la ecuación x²+y²=9, se obtiene la relación r²=9.

De tal manera que, para determinar el valor del radio, simplemente se debe despejar “r” de la igualdad. Al despejar “r”, se obtiene lo siguiente:

De esta manera, se obtiene que el radio de la circunferencia definida por la ecuación x²+y²=9 es r=3.

La siguiente imagen muestra una circunferencia de radio 3 con centro en el origen de coordenadas del plano cartesiano.

Ejercicios de la circunferencia con centro en el origen

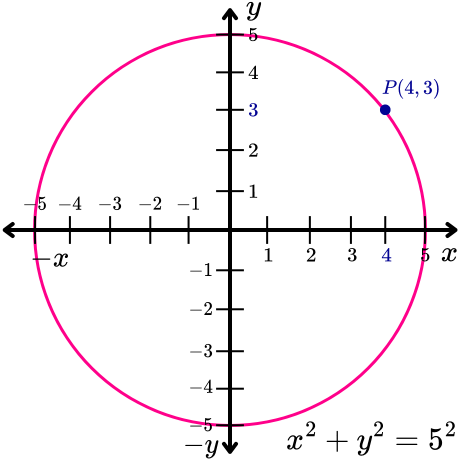
Ejercicio resuelto 3. Encuentra la ecuación de la circunferencia con centro en el origen que pasa por el punto P de coordenadas (4, 3).

Solución: Para hallar la ecuación de una circunferencia con centro en el origen que pasa por un punto P, es necesario conocer el valor del radio de la circunferencia.

Dado que la circunferencia pasa por el punto de coordenadas (4, 3), las coordenadas de este punto satisfacen la ecuación x²+y²=r². Al sustituir las coordenadas de este punto en la ecuación, se obtiene el valor del radio de la circunferencia.

Al resolver para "r", se obtiene el valor del radio de la circunferencia:

Por lo tanto, el radio de la circunferencia que pasa por el punto P de coordenadas (4, 3) es r=5. Ahora, al sustituir este valor en la ecuación de la circunferencia con centro en el origen, se obtiene lo siguiente:

De esta manera, la ecuación de la circunferencia con centro en el origen que pasa por el punto P de coordenadas (4, 3) es x²+y²=25.

La siguiente imagen muestra una circunferencia con centro en el origen que pasa por el punto P de coordenadas (4, 3).

Ejercicio resuelto 4. Comprueba si el punto Q de coordenadas (5, 6) pertenece a la circunferencia cuya ecuación está definida como x²+y²=61.

Solución: Para comprobar si un punto pertenece a una circunferencia, se debe verificar que las coordenadas de dicho punto satisfagan la ecuación de la circunferencia dada.

Como las coordenadas del punto son (5, 6), al sustituir estas coordenadas en la ecuación x²+y²=61, se obtiene lo siguiente:

Como la igualdad es verdadera, el punto de coordenadas (5, 6) pertenece a la circunferencia cuya ecuación es x²+y²=61.

Para más información acerca de cómo hallar la ecuación de una circunferencia con centro en el origen de coordenadas puedes consultar el artículo La circunferencia dados el centro y el radio del portal Prometeo.