Dicciomat

Circunferencia con centro fuera del origen

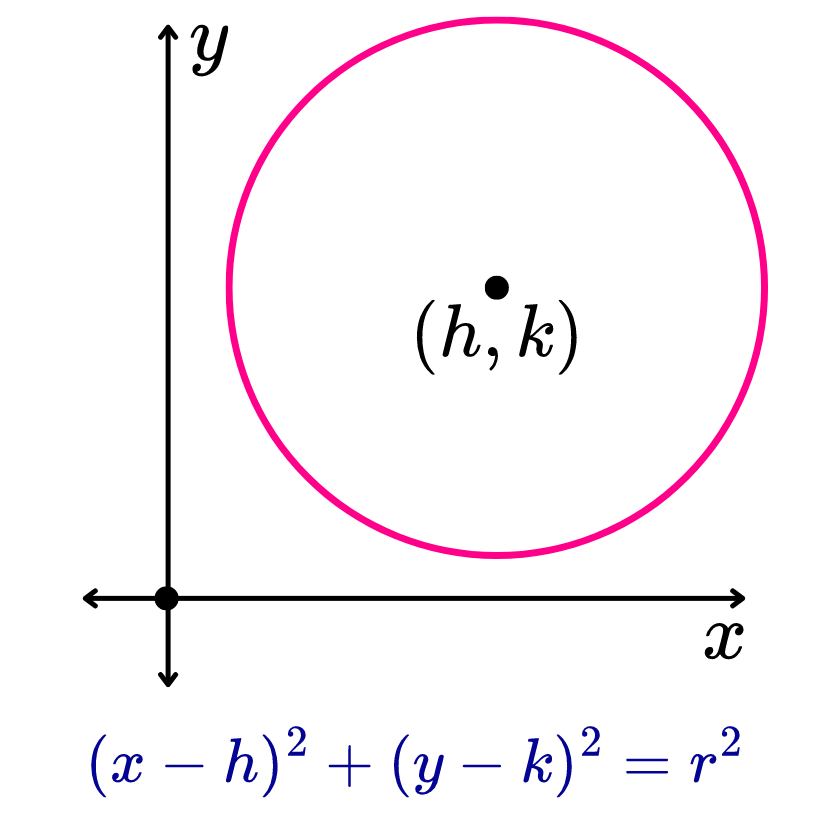
Circunferencia con centro fuera del origen de coordenadas.

Una circunferencia con centro fuera del origen es aquella cuyo centro se encuentra en cualquier otro punto que no sea el origen de coordenadas (0, 0) del plano cartesiano.

En un sistema de coordenadas cartesianas, una circunferencia con centro en el punto de coordenadas (h, k) y radio "r" consta de todos los puntos de coordenadas (x, y) que satisfacen la ecuación (x-h)2+(y-k)2=r2.

Esta ecuación recibe el nombre de ecuación de la circunferencia con centro fuera del origen o ecuación ordinaria de la circunferencia.

Tabla de contenido

Ecuación de la circunferencia con centro fuera del origen

La ecuación de la circunferencia con centro fuera del origen, también llamada ecuación ordinaria de la circunferencia está definida de la siguiente manera:

\[(x-h)^2+(y-k)^2=r^2\]

En esta ecuación, “x” y “y” corresponden a las coordenadas (x, y) de cualquier punto de la circunferencia. Además, “h” y “k” corresponden a las coordenadas del centro (h, k) de la circunferencia, y “r” corresponde al valor del radio de la circunferencia.

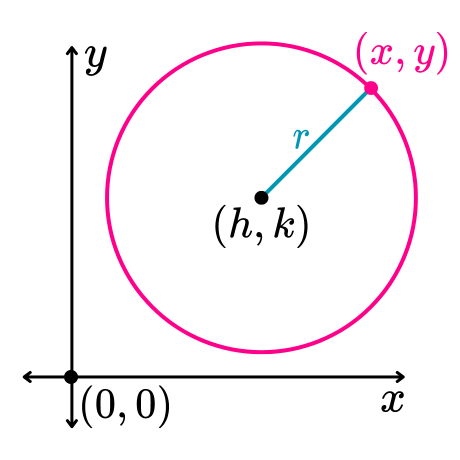
Circunferencia con centro fuera del origen de coordenadas del plano cartesiano

Cómo determinar la ecuación de la circunferencia con centro fuera del origen

Para determinar la ecuación de la circunferencia con centro fuera del origen (ecuación ordinaria de la circunferencia), es necesario conocer las coordenadas del centro (h, k) de la circunferencia y el valor del radio de la circunferencia.

Al sustituir las coordenadas del centro de la circunferencia y el valor del radio en la ecuación (x-h)2+(y-k)2=r2, se obtiene la ecuación de la circunferencia con centro fuera del origen (ecuación ordinaria de la circunferencia).

Ejemplos

Ejemplo 1. Determina la ecuación ordinaria de una circunferencia con centro en (-3, 4) y radio igual a 6.

Solución. La ecuación ordinaria de la circunferencia corresponde a la ecuación de la circunferencia con centro fuera del origen, la cual está definida como (x-h)2+(y-k)2=r2. En esta ecuación, (h, k) corresponde a las coordenadas del centro de la circunferencia y “r” al radio de la circunferencia.

Dado que las coordenadas del centro de la circunferencia son (-3, 4), se tiene que h=-3 y k=4. Además, como el radio de la circunferencia es 6, entonces se tiene que r=6.

Al sustituir estos valores en la ecuación ordinaria (x-h)2+(y-k)2=r2, se obtiene lo siguiente:

\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2\\(x-(-3))^2+(y-4)^2&=6^2\\(x+3)^2+(y-4)^2&=36\end{aligned}\]

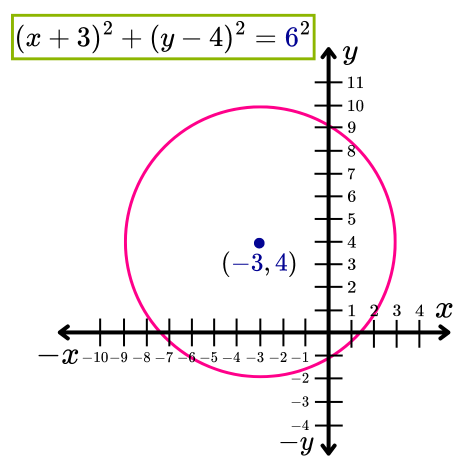
Por lo tanto, la ecuación ordinaria de la circunferencia con centro en (-3, 4) y radio r=6 es (x+3)2+(y-4)2=36.

La siguiente imagen muestra una circunferencia con centro en (-3, 4) y radio 6.

Circunferencia con centro fuera del origen. Circunferencia con centro en (-3, 4) y radio 6.

Ejemplo 2. Obtener la ecuación ordinaria de una circunferencia con centro en (-1, -4) y radio 9.

Solución. Para obtener la ecuación ordinaria de una circunferencia dados su centro y su radio, simplemente se deben sustituir las coordenadas del centro (h, k) y el valor del radio “r” de la circunferencia en la ecuación (x-h)2+(y-k)2=r2.

Como las coordenadas del centro de la circunferencia son (-1, -4), entonces se tiene que h=-1 y k=-4. Además, como el valor del radio de la circunferencia es 9, se tiene que r=9.

Al sustituir estos valores en la ecuación (x-h)2+(y-k)2=r2, se obtiene lo siguiente:

\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2\\(x-(-1))^2+(y-(-4))^2&=9^2\\(x+1)^2+(y+4)^2&=81\end{aligned}\]

Por lo tanto, la ecuación ordinaria de una circunferencia con centro en (-1, -4) y radio 9 está definida como (x+1)2+(y+4)2=81.

Ejercicios resueltos

Ejercicio resuelto 1. Hallar la ecuación ordinaria de una circunferencia con centro en (0, 8) y diámetro 12.

Solución: Para hallar la ecuación ordinaria de una circunferencia es necesario conocer tanto las coordenadas del centro de la circunferencia como el valor del radio de la circunferencia.

Como en este caso se conocen las coordenadas del centro de la circunferencia, pero no el radio de la circunferencia primero debe hallarse el valor del radio.

Dado que la longitud del radio de una circunferencia es la mitad de la longitud del diámetro, entonces si el diámetro de la circunferencia es de 12, la longitud del radio es de 6.

Ahora bien, como las coordenadas del centro de la circunferencia son (0, 8), entonces se tiene que h=0 y k=8. Además, como el radio de la circunferencia es 6, se tiene que r=6.

Al sustituir estos valores en la ecuación ordinaria de la circunferencia, se obtiene lo siguiente:

\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2\\(x-0)^2+(y-8)^2&=6^2\\x^2+(y-8)^2&=36\end{aligned}\]

Por lo tanto, la ecuación ordinaria de la circunferencia con centro en (0, 8) y radio r=6 es x2+(y-8)2=36.

Ecuación ordinaria de la circunferencia ejercicios resueltos

Ejercicio resuelto 2. Obtener la ecuación ordinaria de la circunferencia con centro en (3, -4) y que pasa por el punto P de coordenadas (6, 12).

Solución. Para hallar la ecuación ordinaria de la circunferencia (ecuación de la circunferencia con centro fuera del origen) definida por (x-h)2+(y-k)2=r2, es necesario conocer las coordenadas del centro (h, k) y el valor del radio “r” de la circunferencia.

En este caso, únicamente se conocen las coordenadas del centro de la circunferencia, pero no se conoce explícitamente el valor del radio, por lo que primero debe calcularse el radio de la circunferencia.

Como el valor del radio de una circunferencia corresponde a la distancia que hay entre el centro y un punto de la circunferencia, entonces debe calcularse la distancia que hay entre los puntos (3, -4) y (6, 12).

La fórmula para calcular la distancia entre dos puntos A y B de coordenadas (x1, y1) y (x2, y2) respectivamente, está definida como:

\[D=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\]

Al sustituir las coordenadas de los puntos (3, -4) y (6, 12) en la fórmula anterior, se obtiene lo siguiente:

\[\begin{aligned}D&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\&=\sqrt{(6-3)^2+(12-(-4))^2}\\&=\sqrt{(3)^2+(16)^2}\\&=\sqrt{9+256}\\&=\sqrt{265}\end{aligned}\]

De esta manera, el radio de la circunferencia con centro en (3, -4) y que pasa por el punto P de coordenadas (6, 12) es r=√265.

Ahora que se conocen las coordenadas del centro y el valor del radio de la circunferencia, puede hallarse la ecuación ordinaria de la circunferencia.

Como las coordenadas del centro de la circunferencia son (3, -4), se tiene que h=3 y k=-4. Además, el valor del radio de la circunferencia es r=√265.

Al sustituir estos valores en la ecuación (x-h)2+(y-k)2=r2, se obtiene lo siguiente:

\[\begin{aligned}(x-h)^2+(y-k)^2&=r^2\\(x-3)^2+(y-(-4))^2&=(\sqrt{265})^2\\(x-3)^2+(y+4)^2&=265\end{aligned}\]

Por lo tanto, la ecuación ordinaria de una circunferencia con centro en (3, -4) y que pasa por el punto P de coordenadas (6, 12) es (x-3)2+(y+4)2=265.

Para más información acerca del tema, consulta el artículo Ecuación de la circunferencia con centro fuera del origen dados su centro y radio del portal académico PruébaT.