Ecuación de la recta en la forma pendiente-ordenada al origen
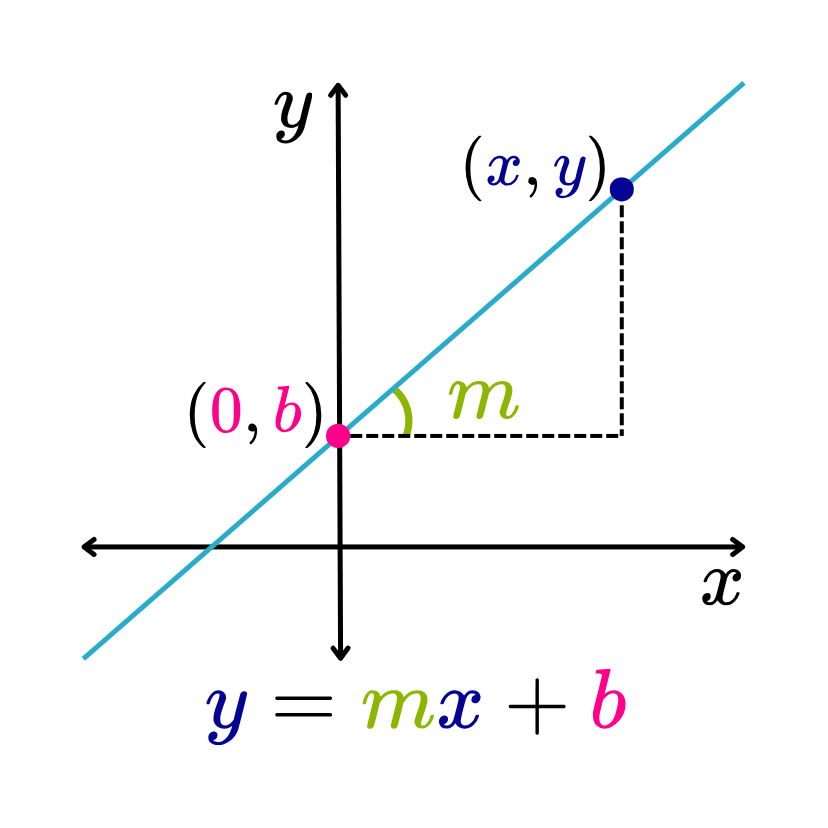
La ecuación de la recta en la forma pendiente-ordenada al origen se define como y=mx+b. En esta ecuación, “m” representa la pendiente de la recta y “b” el valor de la ordenada al origen.
La forma pendiente-ordenada al origen se utiliza para determinar la ecuación de una recta cuando se conocen tanto el valor de la pendiente como el valor de la ordenada al origen.
A esta forma de la ecuación de la recta también se le denomina forma ordinaria de la ecuación de la recta.
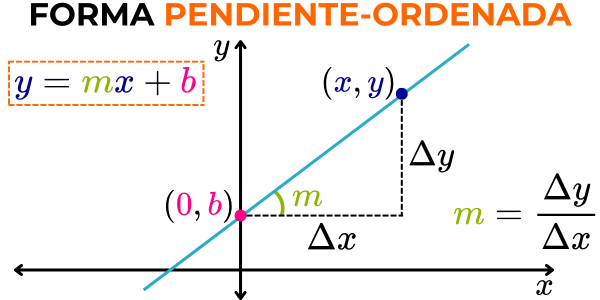
A continuación, se describe en detalle qué es la ordenada al origen, de dónde proviene la forma pendiente-ordenada al origen y cómo se utiliza para determinar la ecuación de una recta.
Ordenada al origen
Las coordenadas cartesianas (x, y) de un punto P en el plano cartesiano se denominan abscisa y ordenada.
La abscisa es la coordenada horizontal y se representa por la letra “x”, mientras que la ordenada es la coordenada vertical y se representa por la letra “y”.
La ordenada al origen es el valor de la coordenada vertical “y” cuando la coordenada horizontal “x” es igual a cero. Por ejemplo, para un punto P de coordenadas (0, 3), la ordenada al origen es igual a 3, ya que, cuando la abscisa (coordenada horizontal “x”) es igual a cero, la ordenada (coordenada vertical “y”) es igual a 3.
De manera similar, para un punto Q de coordenadas (0, -7), la ordenada al origen es igual a -7, ya que, cuando la abscisa es igual a cero, la ordenada es igual a -7.
En términos geométricos, la ordenada al origen es el valor de la ordenada del punto de coordenadas (x, y) en el cual la recta intercepta al eje vertical (eje de las ordenadas) en el plano cartesiano. Es decir, si una recta intercepta al eje vertical en el punto (0, b), entonces la ordenada al origen de la recta es igual a la coordenada “b”.
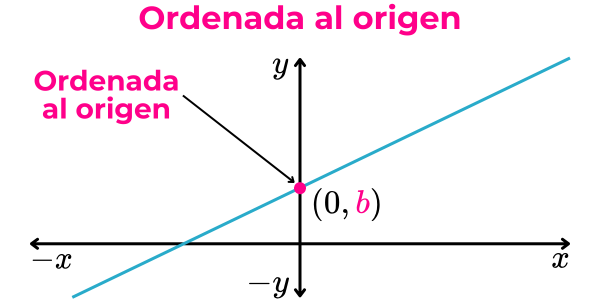
Forma pendiente-ordenada al origen
La ecuación de la recta en la forma pendiente-ordenada al origen se obtiene a partir de la ecuación de la recta en la forma punto-pendiente, la cual está definida de la siguiente manera:
En esta ecuación, “m” corresponde a la pendiente de una recta, y (x1, y1) corresponden a las coordenadas de uno de los puntos por los que pasa la recta.
Si la recta pasa por el punto de coordenadas (0, b), es decir, si la recta intercepta al eje vertical “y” en y=b, entonces la ecuación punto-pendiente de una recta que pasa por el punto de coordenadas (0, b) y cuya pendiente es “m”, está definida como:
Al despejar “y” en esta última igualdad, se obtiene la ecuación de la recta en la forma pendiente-ordenada al origen:
Pendiente-ordenada al origen ejemplos
Ejemplo 1. Determina la ecuación de una recta cuya pendiente es 3 y que intercepta al eje de las ordenadas (eje vertical) en el punto (0, 5).
Solución: Dado que se conoce el valor de la pendiente de la recta y las coordenadas del punto en el que esta intercepta al eje de las ordenadas, es decir, se conoce el valor de la ordenada al origen, entonces puede hallarse la ecuación de la recta en la forma pendiente-ordenada al origen.
Para determinar esta ecuación simplemente se deben sustituir tanto el valor de la pendiente de la recta como el valor de la ordenada al origen en la ecuación pendiente-ordenada al origen, definida como:
En este caso, se tiene que la pendiente de la recta es igual a 3 y, como la recta intercepta al eje vertical y en el punto (0, 5), entonces la ordenada al origen es b=5. Al sustituir estos valores en la ecuación se obtiene lo siguiente:
Por lo tanto, la ecuación de la recta cuya pendiente es 3 y que intercepta al eje de las ordenadas en el punto (0, 5) está definida como y=3x+5.
Ejemplos
Ejemplo 2. Encuentra la ecuación de una recta cuyo valor de la pendiente es m=2/3 y que intercepta al eje vertical en el punto (0, -2).
Solución: Dado que se conoce tanto el valor de la pendiente como las coordenadas del punto de intersección de la recta con el eje vertical (eje de las ordenadas), entonces se puede hallar la ecuación de la recta en la forma pendiente-ordenada al origen.
Para hallar dicha ecuación de la recta, simplemente se deben sustituir el valor de la pendiente y el valor de la ordenada al origen en la ecuación:
En este caso, se tiene que la pendiente de la recta es m=2/3 y, como la recta intercepta al eje vertical en el punto (0, -2), entonces la ordenada al origen es b=-2. Al sustituir estos valores en la ecuación pendiente-ordenada al origen, se obtiene lo siguiente:
Por lo tanto, la ecuación de la recta cuyo valor de la pendiente es m=2/3 y que intercepta al eje vertical en el punto (0, -2) es:
Ejercicios resueltos
Ejercicio resuelto 1. Encuentra el valor de la ordenada al origen de una recta definida por la ecuación y=2x-1.
Solución: Dado que el valor de la ordenada al origen corresponde al valor de la coordenada vertical “y” cuando la coordenada horizontal “x” es igual a cero, para hallar el valor de la ordenada simplemente se debe sustituir x=0 en la ecuación y resolver para “y”.
Al sustituir x=0 en la ecuación y resolver para “y”, se obtiene lo siguiente:
Por lo tanto, la ordenada al origen de una recta definida por la ecuación y=2x-1 es igual a -1.