Ecuación de la recta en la forma punto-pendiente
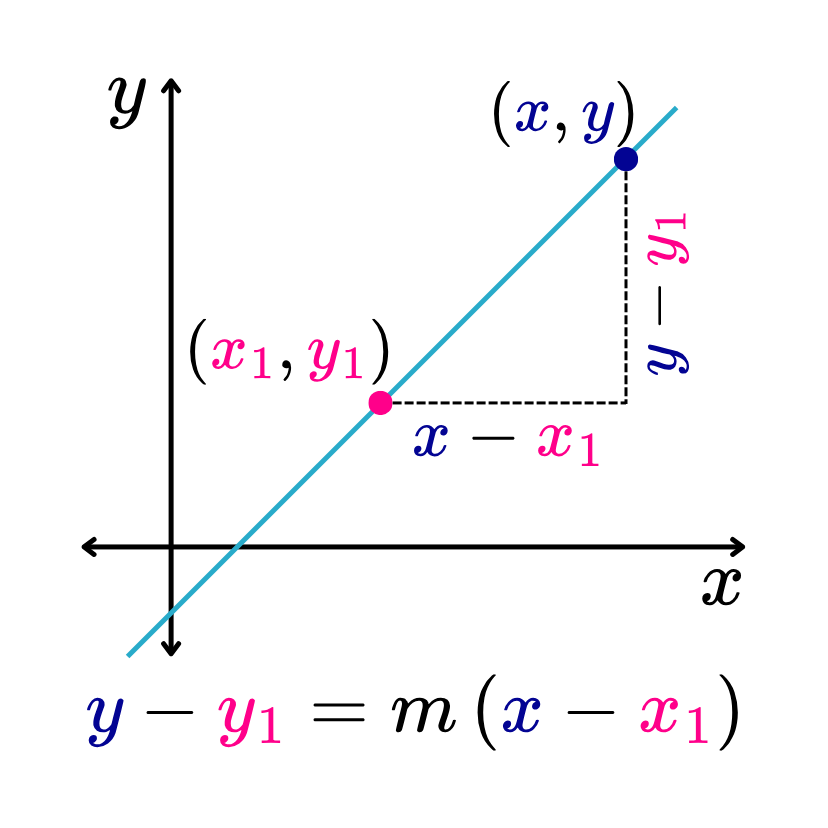
La ecuación de la recta en la forma punto-pendiente está definida como y-y1=m(x-x1).
En esta ecuación, “m” corresponde al valor de la pendiente de la recta, y (x1, y1) corresponden a las coordenadas de uno de los puntos por los que esta pasa.
La forma punto-pendiente se utiliza para determinar la ecuación de una recta cuando se conocen el valor de la pendiente y las coordenadas de uno de los puntos por los que esta pasa.

A continuación, se describe en detalle de dónde proviene la forma punto-pendiente y cómo se utiliza para determinar la ecuación de una recta.
Forma punto-pendiente
La ecuación de la recta en la forma punto-pendiente se obtiene a partir de la fórmula para calcular la pendiente de una recta que pasa por dos puntos, la cual está definida de la siguiente manera:
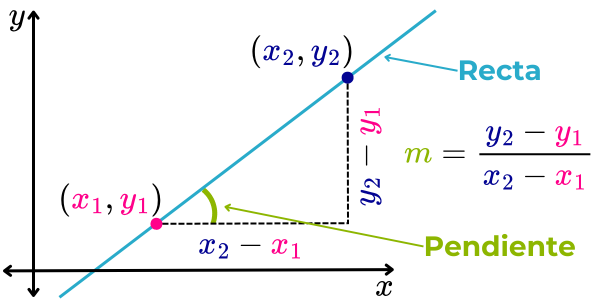
En esta ecuación, “m” representa la pendiente de la recta y (x1, y1), (x2, y2) corresponden a las coordenadas de dos de los puntos por los que esta pasa.
Para deducir la forma punto-pendiente de la ecuación de la recta a partir de la fórmula de la pendiente de una recta que pasa por dos puntos de coordenadas (x1, y1) y (x2, y2), simplemente se despeja "m".
Al multiplicar y reordenar los términos de la igualdad, se obtiene lo siguiente:
Si (x2, y2) son las coordenadas de cualquier punto por el que pasa la recta, entonces estas pueden representarse simplemente como (x, y). De este modo, la forma punto-pendiente de la ecuación de la recta se define de la siguiente manera:
Ecuación de la recta en la forma punto-pendiente ejemplos
Ejemplo 1. Determina la ecuación de la recta que pasa por el punto P de coordenadas (1, 5) y cuyo valor de la pendiente es 2.
Solución: Dado que se conocen las coordenadas de uno de los puntos por los que pasa la recta y también se conoce el valor numérico de la pendiente, entonces puede hallarse la ecuación de la recta en la forma punto-pendiente.
Para determinar la ecuación de la recta en la forma punto-pendiente, simplemente se deben sustituir las coordenadas del punto por el que pasa la recta y el valor de la pendiente en la ecuación punto-pendiente, definida como:
En este caso, la pendiente de la recta es m=2, y las coordenadas del punto (x1, y1) son x1=1 y y1=5. Al sustituir estos valores en la ecuación punto-pendiente, se obtiene lo siguiente:
Por lo tanto, la ecuación de la recta que pasa por el punto P de coordenadas (1, 5) y cuya pendiente es m=2, está definida como: y-5=2(x-1).
Ejemplos
Ejemplo 2. Encuentra la ecuación de una recta que pasa por un punto de coordenadas (-3, -1) y cuya pendiente es 3/5.
Solución: Como se conocen las coordenadas de uno de los puntos por los que pasa la recta y además se conoce el valor numérico de su pendiente, entonces se puede hallar la ecuación de la recta en la forma punto-pendiente.
Para hallar la ecuación de la recta en la forma punto-pendiente, simplemente se deben sustituir las coordenadas del punto por el que pasa la recta y el valor de la pendiente en la ecuación punto-pendiente, definida como:
En este caso, el valor de la pendiente de la recta es m=3/5, y las coordenadas del punto por el que pasa son x1=-3 y y1=-1. Al sustituir estos valores en la ecuación y simplificar la expresión, se obtiene lo siguiente:
Por lo tanto, la ecuación de la recta que pasa por el punto de coordenadas (-3, -1) y cuya pendiente es m=3/5, está definida como:
Ecuación de la recta en su forma punto pendiente ejercicios resueltos
Ejercicio resuelto 1. Determina la ecuación de la recta en la forma punto-pendiente de una recta que pasa por los puntos (-2, -3) y (4, 2).
Solución: Para hallar la ecuación de una recta en la forma punto-pendiente, es necesario conocer tanto el valor de la pendiente de la recta como las coordenadas de uno de los puntos por los que esta pasa.
Dado que en este caso se conocen únicamente las coordenadas de dos puntos por los que pasa la recta, primero es necesario determinar el valor de la pendiente de la recta.
La fórmula para calcular la pendiente de una recta que pasa por dos puntos de coordenadas (x1, y1) y (x2, y2) está definida de la siguiente manera:
Al sustituir las coordenadas de los puntos por los que pasa la recta y simplificar la expresión, se obtiene lo siguiente:
De esta manera, se obtiene que la pendiente de la recta que pasa por los puntos (-2, -3) y (4, 2) es m=5/6.
Ahora que se conoce tanto el valor numérico de la pendiente de la recta como las coordenadas de uno de los puntos por los que pasa, se puede hallar la ecuación de la recta en la forma punto-pendiente:
Como el valor de la pendiente de la recta es m=5/6 y las coordenadas de uno de los puntos por los que pasa son x1=4 y y1=2, al sustituir estos valores en la ecuación punto-pendiente y simplificar la expresión, se obtiene lo siguiente:
Por lo tanto, la ecuación de la recta en la forma punto-pendiente de una recta que pasa por los puntos (-2, -3) y (4, 2) se expresa de la siguiente manera:
Preguntas frecuentes
La ecuación de la recta punto-pendiente es y-y₁=m(x-x₁). En esta ecuación, m es la pendiente y (x, y) son las coordenadas de un punto de la recta.
Se utiliza cuando se conocen tanto el valor de la pendiente y las coordenadas de un punto de la recta.
Se utiliza para determinar la ecuación de una recta cuando se conoce el valor numérico de la pendiente y las coordenadas de un punto perteneciente a la recta.