Dicciomat

Ecuación general de la recta: Características y ejemplos

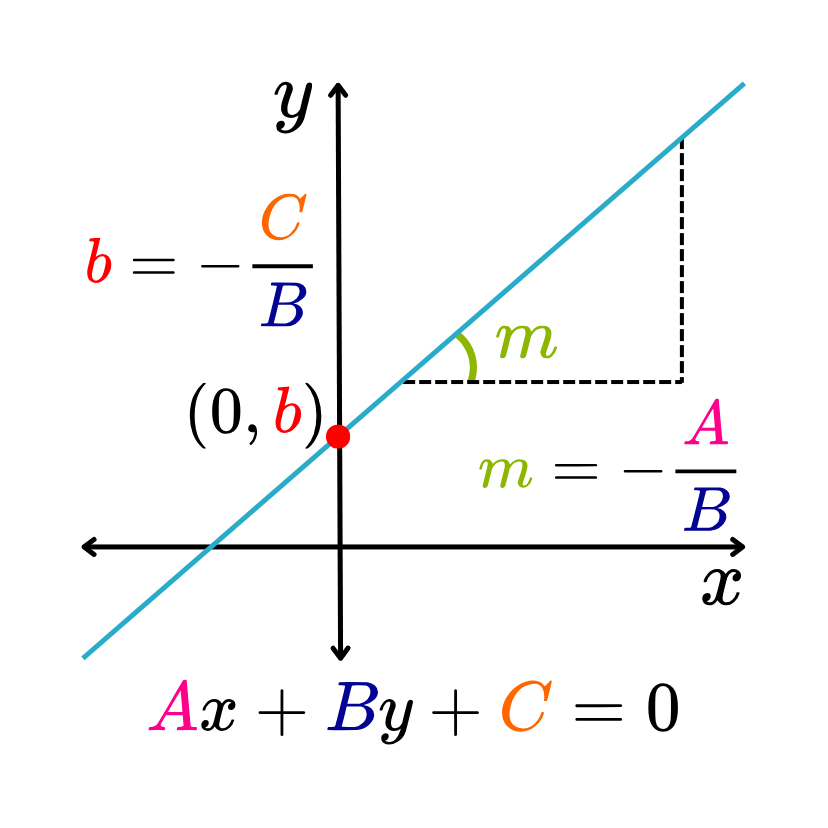
ecuación general de una recta

La ecuación general de la recta es una ecuación de primer grado, definida como Ax+By+C=0.

En esta ecuación, tanto los coeficientes A y B como el término independiente C son números reales, con la condición de que los coeficientes A y B no sean simultáneamente iguales a cero.

Tabla de contenido

La ecuación general de la recta

Si A, B y C son números reales, con la condición de que A y B no sean simultáneamente iguales a cero, la ecuación general de la recta, también conocida como ecuación implícita de la recta o ecuación de la recta en su forma general, se define como Ax+By+C=0.

Dependiendo de los valores de los coeficientes A y B, y del término constante C, la ecuación Ax+By+C=0 representa cualquier tipo de recta en el plano cartesiano, ya sea una recta inclinada, una recta vertical o una recta horizontal.

Ecuación general de la recta: ejemplos

La ecuación general de la recta es una ecuación de primer grado que se emplea para representar cualquier recta en el plano cartesiano.

Por ejemplo, la ecuación 7x+4y-35=0 representa una recta en el plano cartesiano cuya pendiente es -7/4 y cuyo punto de intersección con el eje vertical “y” es el punto de coordenadas (0, 5).

Por otra parte, la ecuación 3x-y+6=0 representa una recta en el plano cartesiano cuya pendiente es m=3 y cuyo punto de intersección con el eje de las ordenadas (eje vertical “y”) es el punto de coordenadas (0, -2).

Deducción de la ecuación general de la recta

Para deducir la ecuación general de la recta, también conocida como ecuación implícita o ecuación en su forma general, considera la ecuación simétrica de la recta, la cual está definida de la siguiente manera:

\[\frac{x}{a}+\frac{y}{b}=1\]

Al multiplicar ambos miembros de la igualdad por el producto a·b, se obtiene lo siguiente:

\[\begin{aligned}\frac{x}{a}+\frac{y}{b}&=1\\a\cdot b\left(\frac{x}{a}+\frac{y}{b}\right)&=a\cdot b(1)\\\frac{a\cdot b\cdot x}{a}+\frac{a\cdot b\cdot y}{b}&=a\cdot b\\b\cdot x+a\cdot y&=a\cdot b\\b\cdot x+a\cdot y-a\cdot b&=0\end{aligned}\]

Al intercambiar los nombres de los coeficientes, de tal manera que b=A, a=B y a·b=C, se obtiene la siguiente ecuación:

\[Ax+By+C=0\]

Esta es la ecuación de la recta en su forma general.

Ecuación implícita de la recta

A la ecuación general de la recta, definida como Ax+By+C=0, también se le denomina ecuación implícita debido a que no está resuelta de manera explícita para ninguna de las variables. Es decir, tanto la variable “x” como la variable “y” están relacionadas entre sí, pero ninguna de las dos está aislada. Esto significa que la relación entre ambas variables está implícita dentro de la ecuación.

En contraste, una ecuación explícita de la recta, como la ecuación de la recta en forma pendiente-ordenada al origen, definida como y=mx+b, muestra la variable “y” en términos de la variable “x”. Es decir, la variable “y” está despejada, lo que facilita obtener su valor para cualquier valor asignado a la variable “x”.

A continuación, veamos las características que determinan los diferentes tipos de rectas.

Características de la ecuación general de la recta

Dado que la ecuación general de la recta Ax+By+C=0 representa cualquier tipo de recta en el plano cartesiano, tanto la pendiente de la recta como la ordenada al origen se pueden obtener de la ecuación general de la recta al expresar la variable “y” en términos de la variable “x”.

Al despejar la variable “y” de la ecuación general de la recta, se obtiene lo siguiente:

\[\begin{aligned}Ax+By+C&=0\\By&=-Ax-C\\y&=\frac{-Ax-C}{B}\\y&=-\frac{A}{B}x-\frac{C}{B}\end{aligned}\]

De esta última igualdad, se concluye que la pendiente de la recta está definida como:

\[m=-\frac{A}{B}\]

La ordenada al origen (intersección con el eje vertical “y”) está definida como:

\[b=-\frac{C}{B}\]
ecuación general de la recta

Ecuación de una recta horizontal

Si el coeficiente A en la ecuación general de la recta Ax+By+C=0 es igual a cero, entonces la pendiente de la recta, definida por la expresión m=-A/B, es igual a cero, y la ordenada al origen está dada por la expresión b=-C/B.

Cuando el coeficiente A es igual a cero, la ecuación general de la recta Ax+By+C=0 se reduce a By+C=0. Esta ecuación corresponde a la ecuación de una recta horizontal cuyo punto de intersección con el eje vertical “y” es el punto de coordenadas (0, -C/B).

Ecuación de una recta vertical

Si el coeficiente B en la ecuación general de la recta Ax+By+C=0 es igual a cero, entonces la pendiente de la recta, definida por la expresión m=-A/B, está indefinida, ya que la división entre cero no está definida en el conjunto de los números reales. Por lo tanto, se dice que la pendiente de la recta es infinita o indefinida.

Cuando el coeficiente B es igual a cero, la ecuación general de la recta Ax+By+C=0 se reduce a la expresión Ax+C=0. Esta ecuación corresponde a la ecuación de una recta vertical, cuyo punto de intersección con el eje horizontal “x” es el punto de coordenadas (-C/A, 0).

Ecuación de una recta que pasa por el origen de coordenadas

Si el término independiente C en la ecuación general de la recta Ax+By+C=0 es igual a cero, entonces la ecuación se reduce a la expresión Ax+By=0. Esta ecuación representa una recta cuya pendiente está definida por la expresión m=A/B, y cuya ordenada al origen, definida por la expresión b=-C/B, es igual a cero.

Cuando el término independiente C es igual a cero, la ecuación general de la recta definida como Ax+By+C=0 se simplifica a la expresión Ax+By=0. Esta ecuación corresponde a la ecuación de una recta inclinada que pasa por el origen de coordenadas (0, 0) en el plano cartesiano.