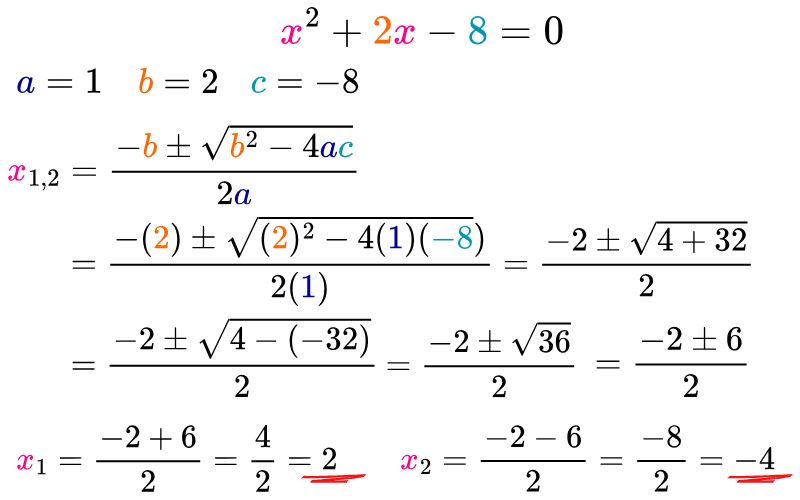Fórmula general para resolver ecuaciones cuadráticas

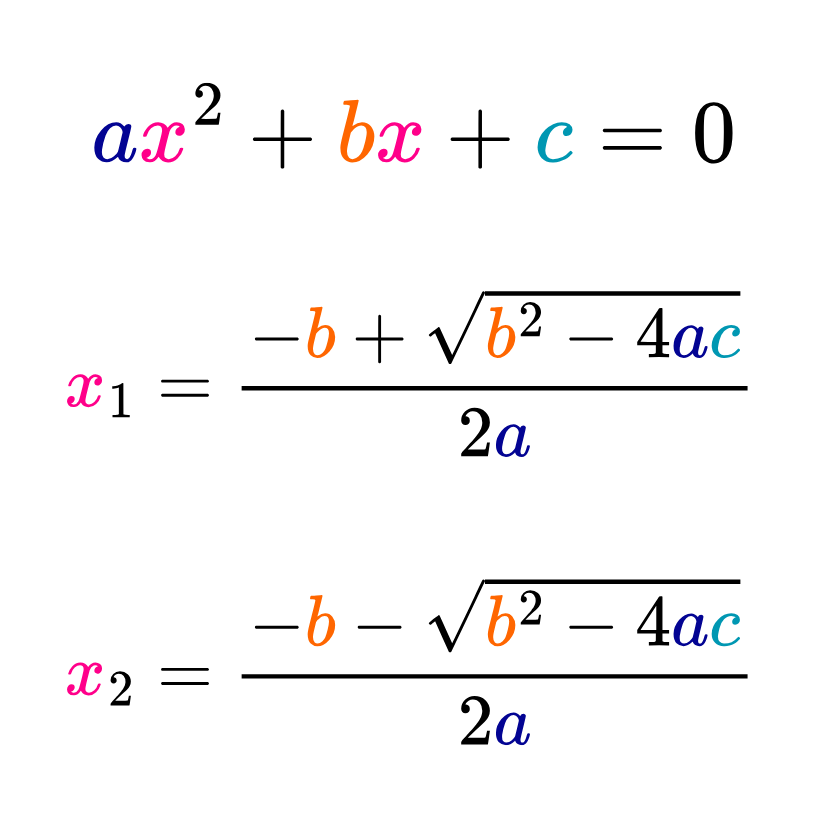
La fórmula general para resolver ecuaciones cuadráticas (ecuaciones de segundo grado) está definida como x_{1, 2}=[-b±√(b²-4ac)]/(2a).

Esta fórmula permite encontrar las soluciones (raíces) de una ecuación cuadrática, es decir, permite determinar el o los valores de "x" que satisfacen la ecuación cuadrática ax²+bx+c=0.

Ecuación cuadrática

Una ecuación cuadrática, también llamada ecuación de segundo grado, es una ecuación algebraica de la forma ax²+bx+c=0.

En esta ecuación, "a", "b" y "c" son números reales, y "a" es diferente de cero.

Una ecuación cuadrática puede tener hasta dos soluciones y, como mínimo, una solución. Estas soluciones pueden ser reales o complejas, es decir, la o las soluciones pueden ser tanto números reales como números complejos.

Para resolver una ecuación cuadrática mediante la fórmula general, es necesario que la ecuación esté en la forma estándar ax²+bx+c=0.

Forma estándar de la ecuación cuadrática

La forma estándar de una ecuación cuadrática es ax²+bx+c=0. En esta ecuación, "a" es el coeficiente del término cuadrático (ax²), "b" es el coeficiente del término lineal (bx), y "c" es el término independiente o término constante de la ecuación.

Los valores de los coeficientes "a", "b" y del término independiente "c" son números reales, y “a” es diferente de cero.

Fórmula general de la ecuación cuadrática

Para resolver una ecuación cuadrática de la forma ax²+bx+c=0, se utiliza la siguiente fórmula:

A esta fórmula se le conoce como fórmula general de la ecuación cuadrática.

Para encontrar la o las soluciones de una ecuación cuadrática, se sustituyen los valores de los coeficientes "a" y "b", así como el valor del término independiente "c", de la ecuación cuadrática ax²+bx+c=0 en la fórmula general.

El número y el tipo de soluciones (raíces) de una ecuación cuadrática dependen del valor del discriminante de la ecuación.

Discriminante de la fórmula general

En la fórmula general, la expresión bajo el símbolo de la raíz cuadrada, b²-4ac, se denomina discriminante de la ecuación cuadrática.

El valor del discriminante proporciona información acerca del número y el tipo de soluciones que tiene una ecuación cuadrática:

• Si el discriminante “b²-4ac” es positivo (mayor que cero), entonces la ecuación cuadrática tiene dos soluciones reales.
• Si el discriminante “b²-4ac” es negativo (menor que cero), entonces la ecuación cuadrática tiene dos soluciones complejas.
• Si el discriminante “b²-4ac” es igual a cero, entonces la ecuación cuadrática tiene una única solución real.

En resumen: Cuando el valor dentro de la raíz cuadrada es positivo, la ecuación tiene dos soluciones reales. Si el valor dentro de la raíz es negativo, no hay soluciones reales, sino soluciones complejas. Si el valor dentro de la raíz es cero, hay una única solución real.

A continuación, veamos los pasos para resolver una ecuación cuadrática usando la fórmula general.

Pasos para resolver una ecuación cuadrática mediante la fórmula general

• Paso 1. Escribir la ecuación cuadrática en la forma estándar ax²+bx+c=0.
• Paso 2. Identificar el valor del coeficiente del término cuadrático “a”, el valor del coeficiente del término lineal “b” y el valor del término independiente “c” de la ecuación cuadrática.
• Paso 3. Sustituir los valores de los coeficientes y del término independiente en la fórmula general.
• Paso 4. Calcular el valor del discriminante para determinar el número y el tipo de soluciones de la ecuación cuadrática.
• Paso 5. Resolver las operaciones para encontrar las soluciones.

A continuación, veamos algunos ejemplos de cómo resolver ecuaciones cuadráticas mediante la fórmula general.