Fracciones propias

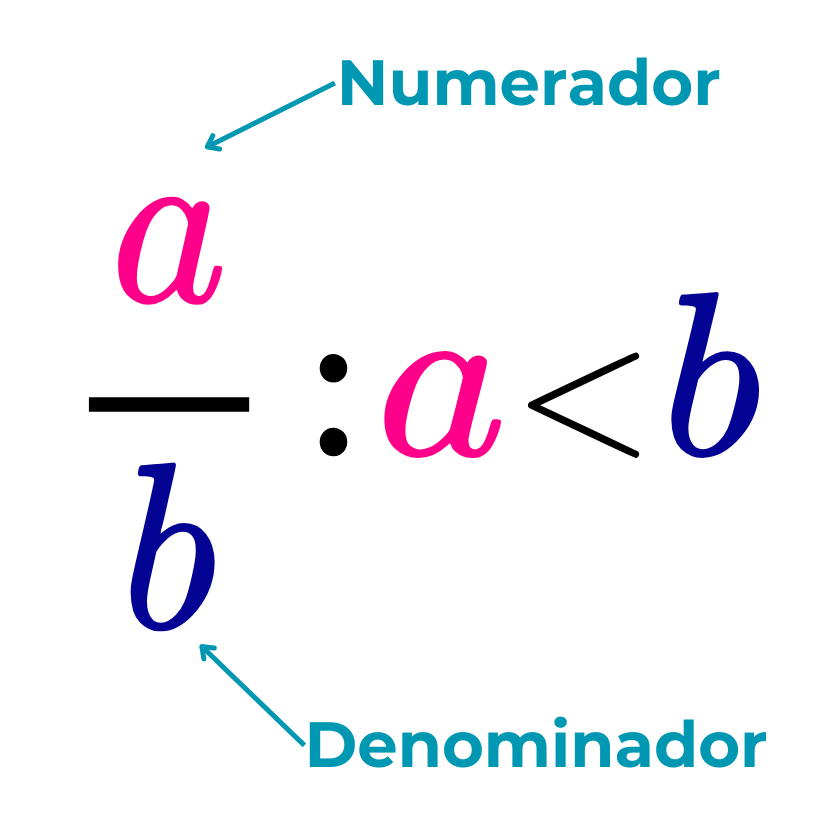
Las fracciones propias son aquellas en las que el numerador es menor que el denominador. Es decir, el número que se encuentra en la parte superior de la línea divisoria es menor que el número ubicado en la parte inferior.

Una de las características importantes de este tipo de fracciones es que representan cantidades mayores a cero y menores que uno. Las fracciones propias son una de los siete tipos de fracciones.

Ejemplos de fracciones propias

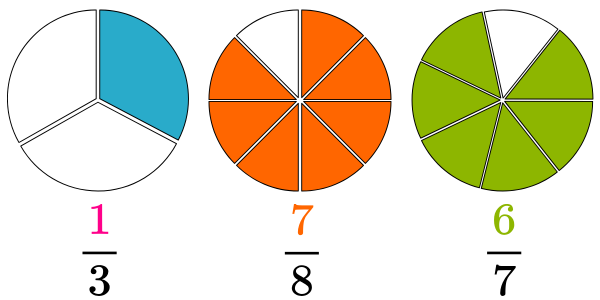
Las fracciones 1/3, 7/8 y 6/7 son fracciones propias, ya que en todas ellas el valor del numerador es menor que el valor del denominador.

¿Qué representa una fracción propia?

Las fracciones propias representan cantidades mayores que cero y menores que la unidad completa. Esto se debe a que, dado que el numerador indica cuántas partes se toman de un entero y el denominador señala cuántas partes iguales forman la unidad completa, entonces al ser el numerador menor que el denominador, siempre se estará tomando solo una parte del total.

Un ejemplo práctico se encuentra al dividir una pizza en 7 porciones iguales. Si una persona consume 4 de esas porciones, esta cantidad se puede expresar con la fracción 4/7 (cuatro séptimos). Esta es una fracción propia, ya que el numerador (4) es menor que el denominador (7). Por lo tanto, esta persona ha consumido una parte menor de la pizza entera, al haber tomado solo 4 de las 7 rebanadas en las que se dividió.

El resultado de una fracción propia siempre es un número mayor que cero y menor que uno. Por ejemplo, la fracción 5/6 (cinco sextos) es una fracción propia, ya que el numerador (5) es menor que el denominador (6). Al efectuar la división 5÷6, se obtiene como resultado el número decimal 0.833, el cual es efectivamente mayor que cero y menor que uno.

Características de las fracciones propias

• El numerador es menor que el denominador.
• Representan una cantidad mayor que cero y menor que uno.
• Una fracción propia es lo opuesto a una fracción impropia.
• Una fracción propia no puede convertirse en una fracción mixta.
• El recíproco (o inverso) de una fracción propia es una fracción impropia.

¿Cómo identificar si una fracción es propia o impropia?

Para identificar si una fracción es propia, se debe comparar el numerador con el denominador. Por ejemplo, la fracción 3/5 es propia, ya que el numerador (3) es menor que el denominador (5).

Por otro lado, la fracción 4/3 no es una fracción propia, ya que el numerador (4) no es menor que el denominador (3). Al contrario, es mayor, por lo que, de acuerdo con las características de las fracciones propias, la fracción 4/3 es una fracción impropia.

Uso de las fracciones propias

Dado que una fracción propia representa siempre una cantidad mayor que cero y menor que uno, este tipo de fracciones se utiliza para expresar una o varias partes de un todo de mayor tamaño.

Por ejemplo, si una pizza entera se divide en 8 partes iguales y alguien consume 3 porciones, se dice que esta persona ha consumido 3/8 (tres octavos) de la pizza. En este caso, la fracción 3/8 es una fracción propia, ya que el numerador (3) es menor que el denominador (8). En otras palabras, esta persona ha consumido una cantidad menor que la pizza entera, ya que solo ha tomado 3 de las 8 rebanadas en las que se dividió la pizza.

Otro ejemplo del uso de las fracciones propias es en la medición de líquidos. Por ejemplo, al medir agua en una jarra graduada, si la capacidad total de la jarra es de 1 litro y esta se llena hasta ¾ de su capacidad (3/4 de litro), se dice que se está utilizando 3/4 de la capacidad total.

Las fracciones propias también se utilizan para medir el tiempo. Por ejemplo, si un programa de televisión dura 60 minutos y ya han pasado 20 minutos, se dice que ha transcurrido 1/3 (un tercio) del programa. Es decir, se ha emitido únicamente una tercera parte de la duración total del programa completo.

Preguntas frecuentes