Función cuadrática: Definición y representación gráfica

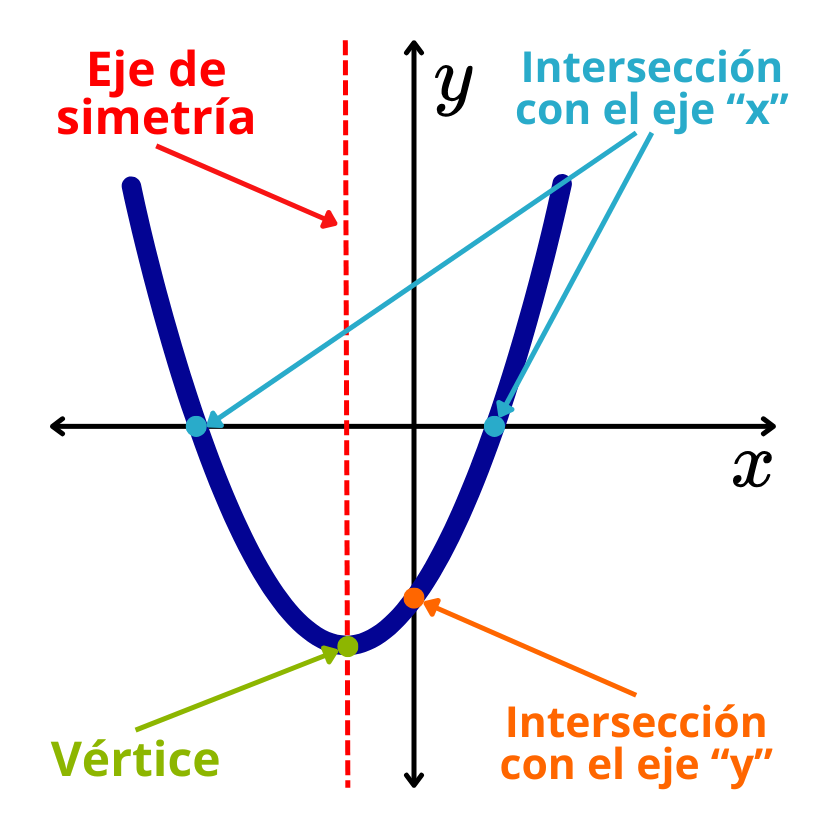
En álgebra, una función cuadrática es una función polinómica en la que el término de grado más alto es de segundo grado.

La gráfica de una función cuadrática es una parábola.

Forma general de la función cuadrática

La forma general de la función cuadrática es f(x)=ax²+bx+c, donde “a”, “b” y “c” son números reales, y “a” es diferente de cero.

Los números “a” y “b” se denominan coeficientes del término cuadrático ax² y del término lineal bx, respectivamente. Al término “c” se le denomina “término independiente” de la función.

La letra “x” representa la variable independiente de la función, y la expresión f(x) representa el valor asociado que se obtiene al reemplazar “x” por algún valor.

Gráfica de la función cuadrática

La gráfica de una función cuadrática f(x)=ax²+bx+c en el plano cartesiano es una parábola.

Las características de la parábola, tales como su orientación, su eje de simetría y los puntos de corte con los ejes de coordenadas, dependen de los valores de los coeficientes “a”, “b” y del término independiente “c” de la función cuadrática.

Orientación de una parábola

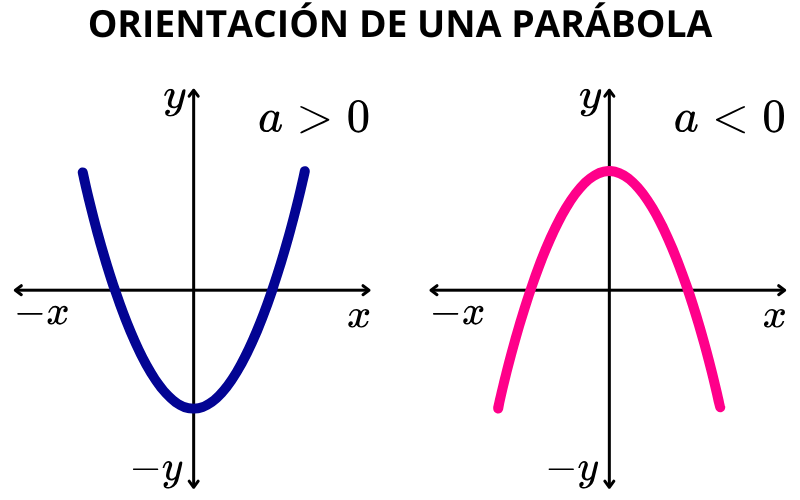
El signo del coeficiente del término cuadrático determina la orientación de la parábola. Es decir, el signo de “a” en la función f(x)=ax²+bx+c indica hacia donde se abre la parábola:

• Si a > 0 , la parábola se abre hacia arriba (forma de ∪).
• Si a < 0 , la parábola se abre hacia abajo (forma de ∩).

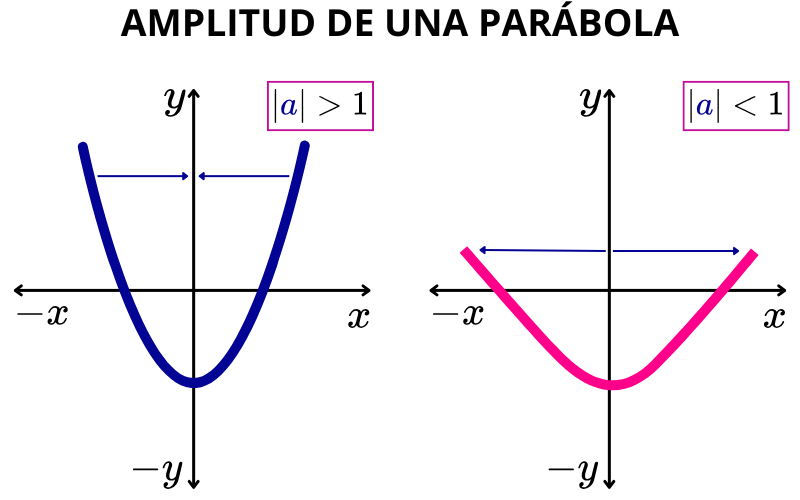
El valor absoluto del coeficiente “a” determina la amplitud de la parábola, es decir, determina que tan abierta o cerrada es una parábola:

• Cuando el valor absoluto de “a” es grande, la parábola es más cerrada.
• Cuando el valor absoluto de “a” es pequeño, la parábola es más abierta.

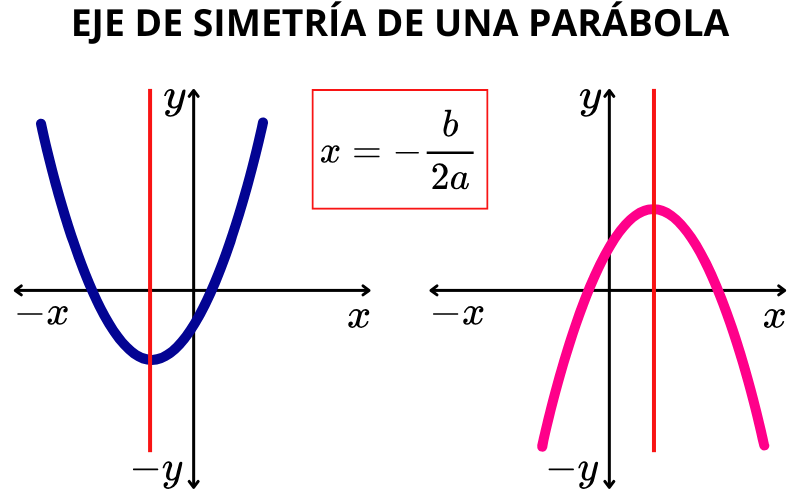
Eje de simetría de una parábola

El eje de simetría de una función cuadrática es una recta vertical paralela al eje “y” que divide la parábola en dos partes iguales.

Una de las características principales del eje de simetría es que pasa por el vértice de la parábola.

La ecuación del eje de simetría está definida de la siguiente manera:

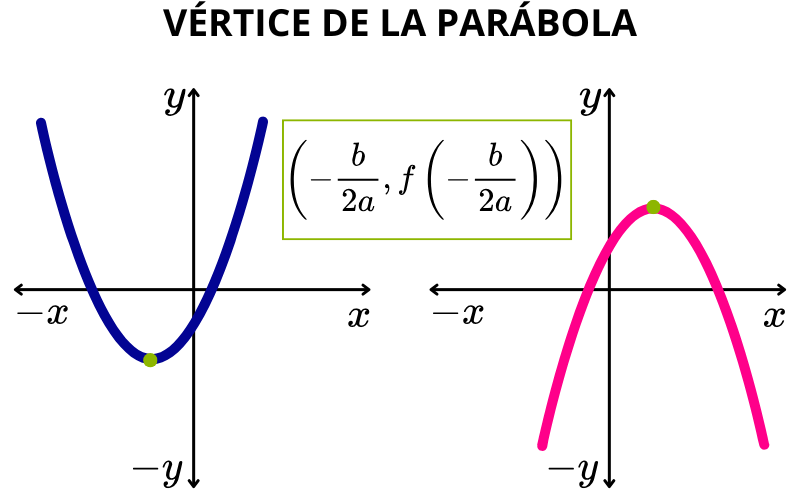
Vértice de una parábola

El vértice de una parábola es el punto donde la parábola intercepta su eje de simetría. Este punto corresponde a un máximo o un mínimo de la función cuadrática.

El vértice es un máximo o un mínimo dependiendo del signo del coeficiente del término cuadrático “a” en la función cuadrática f(x)=ax²+bx+c:

• Si a > 0, el vértice de la parábola corresponde a un punto mínimo de la función cuadrática.
• Si a < 0, el vértice de la parábola corresponde a un punto máximo de la función cuadrática.

Coordenadas del vértice de una parábola

La coordenada horizontal “x” del vértice de la parábola está definida de la siguiente manera:

La coordenada vertical “y” del vértice de la parábola se obtiene al evaluar el valor de la coordenada horizontal “x” en la función, es decir, queda definida de la siguiente manera:

De tal manera que, las coordenadas (x, y) del vértice de la parábola están definidas de la siguiente manera:

Raíces de una función cuadrática

Las soluciones, raíces o ceros de una función cuadrática f(x)=ax²+bx+c son los valores de la variable independiente “x” para los cuales la función es igual a cero, es decir, son los valores de “x” que satisfacen la ecuación f(x)=0.

Para hallar los valores de “x”, se iguala a cero la función cuadrática. Al igualar a cero la función cuadrática f(x)=ax²+bx+c, se obtiene una ecuación cuadrática en su forma estándar ax²+bx+c=0.

Para resolver una ecuación cuadrática en su forma estándar ax²+bx+c=0, se utiliza la siguiente fórmula:

A esta fórmula se le conoce como la fórmula general de la ecuación cuadrática. Esta fórmula permite encontrar las soluciones de una ecuación cuadrática, es decir, las raíces o ceros de la función.

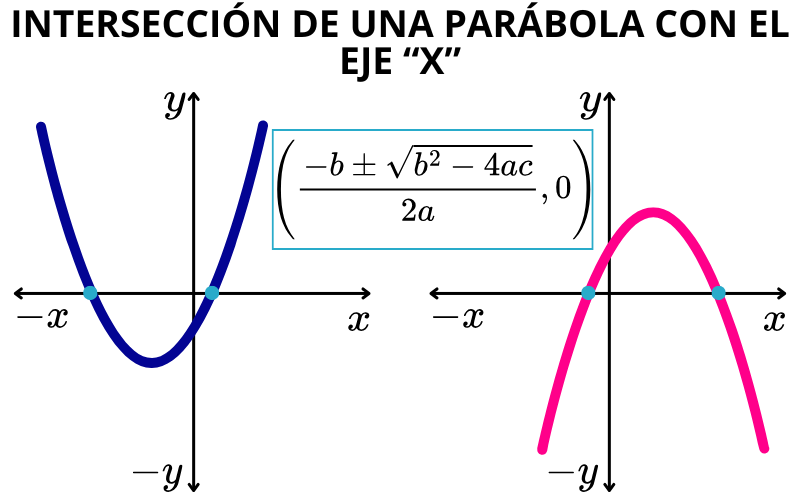
Puntos de corte con el eje horizontal X

Los puntos de corte de la función cuadrática f(x)=ax²+bx+c con el eje horizontal "x" son los puntos de coordenadas (x, 0).

El valor de la coordenada horizontal “x” corresponde a el o los valores de “x” cuando f(x)=0, es decir, el o los valores de “x” son las soluciones de la ecuación cuadrática.

Para determinar la intersección con el eje horizontal, se iguala a cero la función y se resuelve la ecuación cuadrática resultante.

La fórmula general para resolver una ecuación cuadrática en su forma estándar ax²+bx+c=0 está definida de la siguiente manera:

El número y el tipo de soluciones dependen del valor del discriminante de la ecuación cuadrática.

En la fórmula general, la expresión bajo el símbolo de la raíz cuadrada, b²-4ac, se denomina discriminante de la ecuación cuadrática.

El valor del discriminante proporciona información sobre el número y el tipo de soluciones de una ecuación cuadrática:

• Si el discriminante b²-4ac es positivo (mayor que cero), la ecuación cuadrática tiene dos soluciones reales.
• Si el valor del discriminante b²-4ac es negativo (menor que cero), la ecuación cuadrática tiene dos soluciones complejas.
• Cuando el discriminante b²-4ac es igual a cero, la ecuación cuadrática tiene una única solución real.

Por lo tanto, dado que una ecuación cuadrática puede tener dos, una o ninguna solución real, la gráfica de una función cuadrática puede tener dos, uno o ningún punto de corte con el eje horizontal "x".

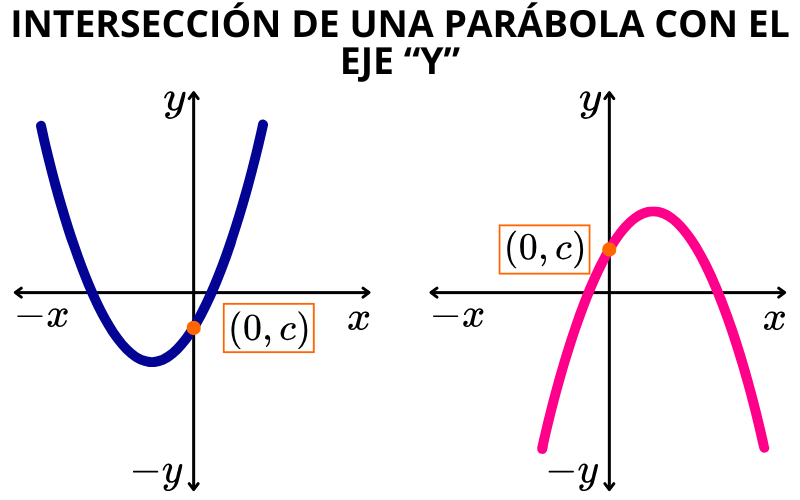
H3. Punto de corte con el eje vertical Y

El punto de corte de la función cuadrática f(x)=ax²+bx+c con el eje vertical "y" es el punto de coordenadas (0, y).

El valor de la coordenada vertical “y” corresponde al valor de f(x) cuando x=0 en la ecuación cuadrática.

Al hacer x=0 en la ecuación cuadrática ax²+bx+c=0, se obtiene que el valor de "y" y este es igual a “c”. De esta manera, la función cuadrática intercepta el eje vertical “y” en el punto (0, c), donde “c” es el término independiente de la función cuadrática f(x)=ax²+bx+c.

En términos geométricos, el valor del término independiente “c” de la función cuadrática f(x)=ax²+bx+c determina el desplazamiento vertical de la parábola con respecto al origen de coordenadas del plano cartesiano.

Cuando el término independiente “c” de una función cuadrática f(x)=ax²+bx+c es igual a cero, la parábola pasa por el origen de coordenadas (0, 0) del plano cartesiano.

Para más información acerca del tema, consulta el artículo "Función cuadrática -Definición y representación gráfica" del sitio "Superprof".