Función matemática: Dominio, codominio y rango
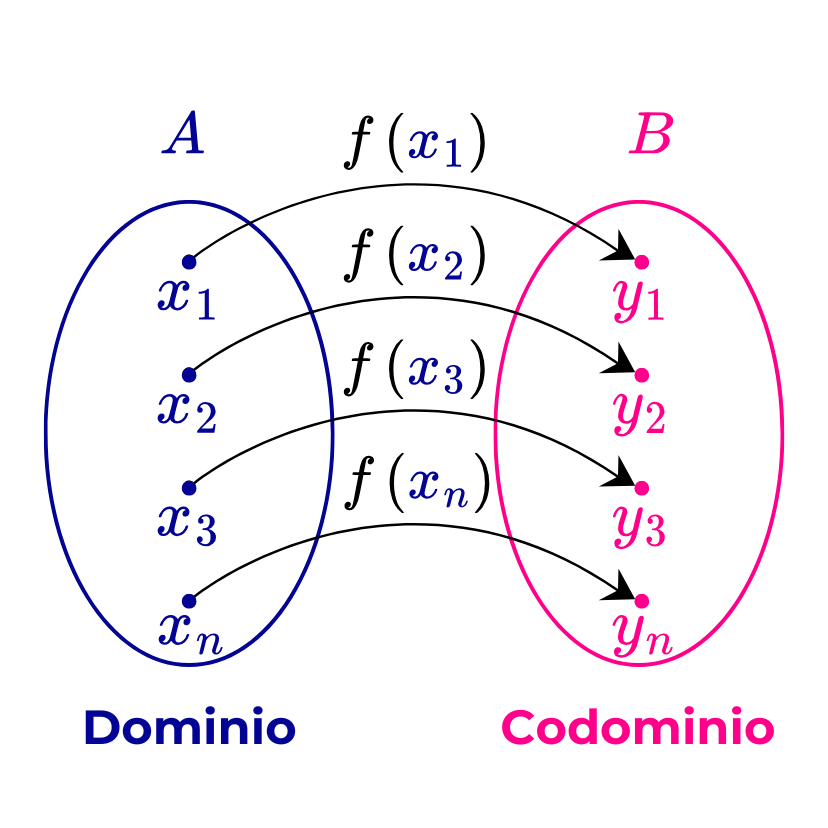
Una función matemática es una regla que asocia a cada elemento de un conjunto "A", denominado dominio, un único elemento de un conjunto "B" denominado codominio.
Definición de función matemática
Una función matemática es una regla que asocia a cada elemento de un conjunto "A" un único elemento de un conjunto "B".
Al conjunto "A" se le denomina dominio de la función y al conjunto "B" se le denomina codominio (o contradominio) de la función.
Una función se denota generalmente con las letras f, g o h , de tal manera que, una función "f" con dominio en "A" y codominio en "B" se escribe de la siguiente manera:
Esta función se representa como f(x)=y, lo cual indica que esta función asocia a cada valor de “x” del dominio (conjunto A ) un único valor de “y” en el codominio (conjunto B ).
Si por ejemplo el dominio y el codominio de una función "f" son el conjunto de todos los números reales, entonces esta función se escribe de la siguiente manera:
De manera similar, si por ejemplo el dominio de una función es el conjunto de todos los números enteros y el codominio es el conjunto de los números enteros positivos, entonces esta función se escribe se la siguiente manera:
Dada una función “f” con dominio en "A" y codominio en "B", la naturaleza de los elementos de estos conjuntos está estrechamente relacionada con la regla de correspondencia de “f”. De tal manera que, el dominio de una función debe ser un conjunto tal que, si “x” es un elemento de dicho conjunto, entonces, mediante la regla de correspondencia, sea posible asignarle un elemento “y” bien definido (y único) en el codominio "B".
Dominio de una función
El dominio de una función “f” es el conjunto formado por todos aquellos valores de “x” para los cuales existe un valor asociado "y", tal que f(x)=y. Es decir, es el conjunto de todos los elementos para los cuales la función está bien definida.
Por ejemplo, considera la función “f” definida como f(x)=1/x. El dominio de esta función es el conjunto de todos los números reales excepto el cero, ya que no existe un valor asociado f(x)=y cuando “x” es igual a cero. Esto se debe a que no se puede dividir una cantidad entre cero.
Por lo tanto, la función f(x)=1/x está bien definida para cualquier valor de “x” excepto cuando “x” es igual a cero. Así, el dominio de esta función es el conjunto de todos los número reales excepto el cero. Matemáticamente, esto se expresa de la siguiente manera:
Codominio de una función
El codominio de una función “f” es el conjunto formado por todos aquellos valores que podrían obtenerse al evaluar todos los elementos del dominio en la función. En otras palabras, el codominio de una función puede incluir elementos que no necesariamente se obtienen al aplicar “f” sobre todos los elementos del dominio.
Por ejemplo, sea “f” una función definida como f(x)=x2 (función cuadrática). En este caso, el dominio de la función es el conjunto de todos los números reales, y el codominio también se establece como el conjunto de todos los números reales, ya que al evaluar cualquier número real en la función se obtiene como resultado otro número real. Sin embargo, observa que al evaluar cualquier número real “x” en la función f(x)=x2, únicamente se obtienen como resultados números reales positivos, ya que el cuadrado de cualquier número real siempre es mayor o igual que cero.
Por lo tanto, el codominio de la función f(x)=x2 se expresa de la siguiente manera:
El conjunto de valores que se obtiene al evaluar todos los elementos del dominio de una función se denomina rango, recorrido o imagen de una función.
Rango, recorrido o imagen de una función
El rango, recorrido o imagen de una función “f” es el conjunto formado por todos aquellos valores de “y” que si se obtienen al evaluar todos los elementos del dominio en la función.
Por ejemplo, en la función f(x)=x2, el rango, recorrido o imagen de dicha función es el conjunto de todos los números reales positivos, además del cero, ya que, al evaluar cualquier número real, positivo o negativo, se obtiene siempre como resultado un número real mayor o igual que cero.
Por lo tanto, el rango de la función f(x)=x2 se expresa de la siguiente manera:
Es importante destacar que la imagen de una función “f” es un subconjunto del codominio de la misma función. Esto significa que el codominio y la imagen no tienen que ser iguales; pueden existir elementos en el codominio que no son la imagen de ningún elemento del dominio.
Preguntas frecuentes
Una función matemática es una regla de asociación entre dos conjuntos. Esta regla asigna a cada elemento de un primer conjunto A un único elemento de un segundo conjunto B. Al conjunto A se le denomina dominio de la función, y al conjunto B, codominio de la función.
En otras palabras, dados un conjunto A y un conjunto B, una función es una regla que asocia a cada elemento del conjunto A (el dominio) un único elemento del conjunto B (el codominio).
El dominio de una función es el conjunto de todos los valores de entrada posibles para los cuales la función está bien definida. En otras palabras, es el conjunto de todos los valores que una variable de entrada “x” puede tomar y que pueden evaluarse en la función sin que se obtenga un resultado indefinido.
Calcular el dominio de una función consiste en hallar todos los valores posibles de la variable “x” para los cuales la función está bien definida. Esto implica identificar y excluir aquellos valores que, al evaluarse en la función, la función no esté definida.
Calcular el rango (o imagen) de una función implica encontrar el conjunto de todos los valores de “y” que se obtienen al evaluar todos los valores del dominio en la función. Uno de los métodos para calcular el rango de una función consiste en despejar la variable “x” de la regla de correspondencia, si es posible; es decir, expresar a la variable “x” en términos de la variable “y” y verificar en la expresión resultante los valores posibles de “y”.