Convertir grados a radianes
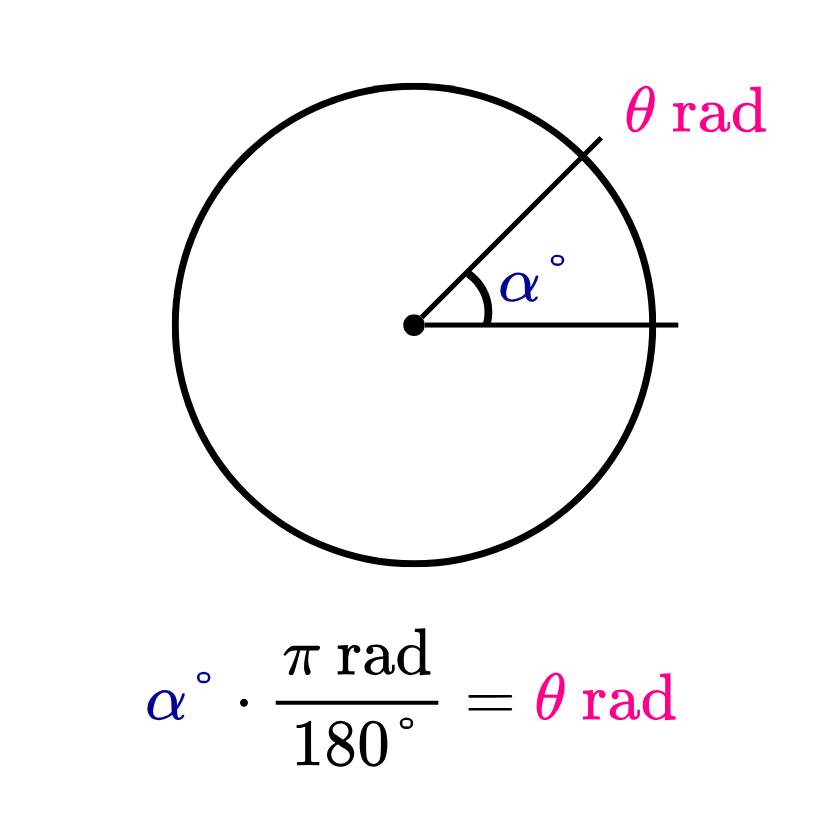
Los grados y los radianes son las dos unidades de medida más comunes para expresar la amplitud de un ángulo. Para convertir grados a radianes, se multiplica el valor del ángulo en grados por π (π radianes) y se divide entre 180°.
En otras palabras, si α representa la amplitud de un ángulo en grados, entonces, para convertirlo a radianes, se multiplica por π y se divide entre 180°. Matemáticamente, esto se expresa de la siguiente manera:
Grados sexagesimales
Los grados sexagesimales son una unidad de medida del sistema sexagesimal. El símbolo de los grados sexagesimales es el grado “°”. La amplitud de un ángulo en grados sexagesimales se representa por el valor numérico de la amplitud del ángulo seguido del símbolo “°”.
Por ejemplo, un ángulo de 90 grados sexagesimales se escribe como 90°. De manera similar, un ángulo de 120 grados se escribe como 120°.
Radianes
Los radianes son una unidad de medida del sistema internacional de unidades (SI). La amplitud de un ángulo en radianes se representa simplemente por el valor numérico de la amplitud seguido de la abreviatura "rad". Por ejemplo, un ángulo de π radianes se escribe como π rad. De manera similar, un ángulo de (2π)/3 radianes se escribe simplemente como (2π)/3 rad.
Fórmula para convertir grados a radianes
La fórmula para convertir de grados a radianes se define de la siguiente manera:
En esta fórmula, α representa la amplitud del ángulo en grados que se desea convertir a radianes, y π es el número irracional pi.

¿Cómo convertir de grados a radianes?
Para convertir de grados a radianes, primero se multiplica el ángulo en grados por π y luego se divide entre 180°. Es decir, si α representa la amplitud de un ángulo en grados, entonces la conversión a radianes se realiza multiplicando el valor de α por π y dividiendo entre 180°.
Cuando se realiza la conversión de grados a radianes, no se utiliza un valor aproximado de π. Esto se debe a que π es un valor exacto. Lo que se hace es expresar la multiplicación del ángulo en grados por π, dividir entre 180° y luego simplificar la fracción resultante a su mínima expresión.
Por ejemplo, para convertir un ángulo de 135° a radianes, primero se multiplica el valor del ángulo en grados por π. Esto se expresa de la siguiente manera:
Luego, se divide esta multiplicación entre 180°:
Finalmente, se simplifica la fracción resultante a su mínima expresión.
Por lo tanto, el ángulo de 135° en radianes es igual a 3π/4 rad.
Ejemplos de cómo convertir grados a radianes
Ejemplo 1: ¿A cuántos radianes equivale un ángulo de 240°?
Solución: La fórmula para convertir de grados a radianes está definida como: (α·π)/180°. En esta fórmula, α representa el valor del ángulo en grados. Al sustituir α=240° en la fórmula y simplificar la expresión, se obtiene lo siguiente:
Por lo tanto, el ángulo de 240° equivale a 4π/3 rad. Al efectuar la división para obtener una aproximación decimal, el ángulo de 240° es aproximadamente 4.1887 radianes.
Ejemplo 2. Convertir 200 grados a radianes.
Solución: Para convertir un ángulo de grados a radianes, se multiplica el valor del ángulo en grados por π y luego la multiplicación se divide entre 180 grados. Matemáticamente, esto se expresa de la siguiente manera:
Al sustituir α=200°, se obtiene lo siguiente:
Por lo tanto, el ángulo de 200° equivale a 10π/9 rad.
Ejemplo 3. Convertir 270 grados a radianes.
Solución: Al sustituir el valor del ángulo en grados en la fórmula para convertir un ángulo de grados a radianes definida como (α·π)/180°, se obtiene lo siguiente:
Por lo tanto, el ángulo de 270° equivale 3π/2 rad.
Tabla de conversión de los ángulos más comunes
La siguiente tabla muestra la conversión de los ángulos más comunes de grados sexagesimales a radianes.
| Ángulo en grados (°) | Ángulo en radianes (rad) |
|---|---|
| 0° | 0 rad |
| 45° | π/4 rad |
| 90° | π/2 rad |
| 135° | 3π/4 rad |
| 180° | π rad |
| 225° | 5π/4 rad |
| 270° | 3π/2 rad |
| 315° | 7π/4 rad |
| 360° | 2π rad |