Leyes de los exponentes

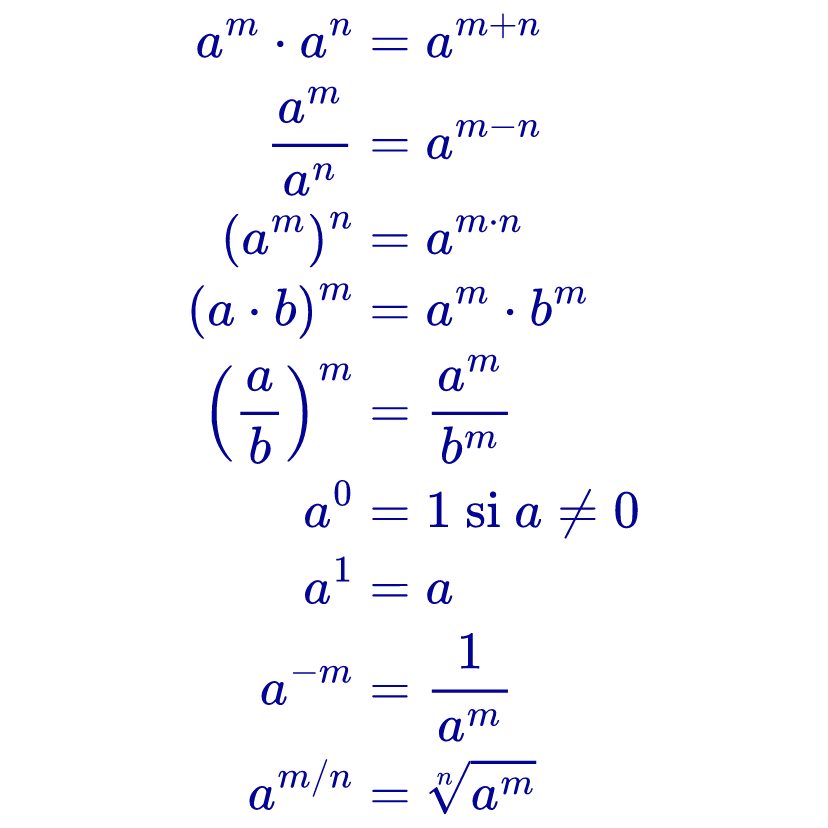
Las leyes de los exponentes son un conjunto de reglas matemáticas que permiten simplificar operaciones con potencias.

Una potencia es una forma abreviada de expresar una multiplicación de números iguales. Se representa como aⁿ. En esta expresión, "a" se denomina base de la potencia y "n" exponente.

La base “a” es el factor que se repite, mientras que el exponente “n” es el número que indica cuántas veces se repite la base como factor. Por ejemplo, la potencia 2³ e lee como "dos elevado al cubo" y significa que la base, en este caso el número 2, se repite como factor 3 veces. Matemáticamente, esto se expresa de la siguiente manera:

\[2^3=2\cdot 2\cdot 2\]

A continuación, presentamos una lista completa de las leyes de las potencias, lo que establece cada una y algunos ejemplos de cómo aplicarlas para simplificar operaciones con potencias.

Tabla de contenido

Ley 1. Potencia de exponente cero
Ley 2. Potencia de exponente uno
Ley 3. Potencia de exponente negativo
Ley 4. Potencia de exponente racional
Ley 5. Multiplicación de potencias con la misma base
Ley 6. División de potencias con la misma base
Ley 7. Potencia de una potencia
Ley 8. Producto elevado a un exponente
Ley 9. Cociente elevado a un exponente
Tabla de la ley de los exponentes
Tabla completa de las leyes de los exponentes

Ley 1. Potencia de exponente cero

Una potencia de exponente cero es aquella de la forma a⁰. Cuando la base de una potencia es diferente de cero y el exponente es igual a cero, la potencia es igual a uno. Matemáticamente, esto se expresa de la siguiente manera:

\[a^0=1\text{ si }a\neq 0\]

Esta ley de los exponentes establece que cualquier número diferente de cero, elevado al exponente cero, siempre es igual a uno.

Por ejemplo, la potencia 3⁰=1, de manera similar, la potencia 2⁰=1, ya que en ambos casos las bases de las potencias son diferentes de cero y los exponentes son iguales a cero.

Ley 2. Potencia de exponente uno

Una potencia de exponente uno es aquella de la forma a¹. Cuando una potencia tiene exponente uno, el resultado es la misma base de la potencia. Matemáticamente, esto se expresa de la siguiente manera:

\[a^1=a\]

Esta segunda ley de los exponentes establece que cualquier número elevado al exponente uno, es igual al mismo número.

Por ejemplo, la potencia 5¹=5, de manera similar, la potencia 7¹=7, ya que en ambos casos los exponentes de las potencias son iguales a uno.

Ley 3. Potencia de exponente negativo

Una potencia de exponente negativo es aquella de la forma a^-m. Una potencia de exponente negativo se define como el recíproco de la potencia, pero con el exponente positivo. Matemáticamente, esto se expresa de la siguiente manera:

\[a^{-m}=\frac{1}{a^m}\]

Esta tercera ley de los exponentes establece que una potencia de exponente negativo es igual al recíproco de la potencia, pero con exponente positivo. En otras palabras, es igual a 1 dividido entre la potencia, pero con exponente positivo.

Por ejemplo, considera la potencia 8^-3. De acuerdo con la ley de potencias con exponente negativo, esta potencia es igual al recíproco de la potencia, pero con exponente positivo, es decir:

\[8^{-3}=\frac{1}{8^3}\]

Ley 4. Potencia de exponente racional

Las potencias de exponente racional son aquellas de la forma a^m/n. Un exponente racional es un número fraccionario de la forma m/n, donde “m” y “n” son números enteros y “n” es diferente de cero.

Una potencia de exponente racional m/n es igual a la raíz enésima de la base de la potencia elevada al exponente “m”. Matemáticamente, esto se expresa de la siguiente manera:

\[a^{m/n}=\sqrt[n]{a^m}\]

Por ejemplo, considera la potencia 9^3/5. De acuerdo con la ley de potencias con exponente racional, esta potencia es igual a la raíz quinta de 9 elevado al cubo, es decir:

\[9^{3/5}=\sqrt[5]{9^3}\]

Ley 5. Multiplicación de potencias con la misma base

Sean a^m y aⁿ dos potencias con la misma base "a". La multiplicación de potencias con la misma base está definida de la siguiente manera:

\[a^m\cdot a^n=a^{m+n}\]

Esta quinta ley de los exponentes establece que cuando se multiplican dos potencias con la misma base, su producto es igual a una potencia con la misma base, elevada a un exponente igual a la suma de los exponentes originales.

Por ejemplo, considera la multiplicación de potencias 2³∙2⁴. Dado que estas potencias tienen la misma base, su producto es igual a una potencia con la misma base y con un exponente igual a la suma de los exponentes originales, es decir:

\[\begin{aligned}2^3\cdot 2^4&=2^{3+4}\\&=2^7\end{aligned}\]

Ley 6. División de potencias con la misma base

Sean a^m y aⁿ dos potencias con la misma base "a". La división de potencias con la misma base está definida de la siguiente manera:

\[\frac{a^m}{a^n}=a^{m-n}\]

Esta sexta ley de los exponentes establece que cuando se dividen dos potencias con la misma base, su cociente es igual a una potencia con la misma base, elevada a un exponente igual a la resta de los exponentes originales.

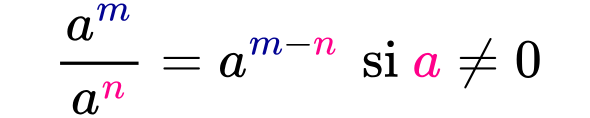
Por ejemplo, considera la división de potencias 6³/6². Como ambas potencias tienen la misma base, su cociente es igual a una potencia con la misma base y con un exponente igual a la diferencia de los exponentes originales, es decir:

\[\begin{aligned}\frac{6^3}{6^2}&=6^{3-2}\\&=6^1\\&=6\end{aligned}\]

Ley 7. Potencia de una potencia

Sea a^m una potencia de base “a” y exponente “m”. Si esta potencia se eleva a un nuevo exponente “n”, los exponentes se multiplican. Matemáticamente, esto se expresa de la siguiente manera:

\[\left(a^m\right)^n=a^{m\cdot n}\]

Esta séptima ley de los exponentes establece que cuando una potencia se eleva a un exponente, se obtiene una potencia con la misma base, elevada a un exponente igual al producto de los exponentes originales.

Por ejemplo, considera la potencia 9². Al elevar esta potencia a un exponente 3, el resultado es igual a una potencia con la misma base y con un exponente igual al producto de los exponentes. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\left(9^2\right)^3&=9^{2\cdot 3}\\&=9^{6}\end{aligned}\]

Ley 8. Producto elevado a un exponente

Cuando un producto de dos o más factores se eleva a un exponente, el resultado es el mismo producto, pero con cada factor elevado al exponente dado. Matemáticamente, esto se expresa de la siguiente manera:

\[\left(a\cdot b\right)^m=a^m\cdot b^m\]

Esta octava ley de los exponentes establece que cuando la base de una potencia es un producto de factores, cada factor se eleva al mismo exponente de la potencia.

Ley 9. Cociente elevado a un exponente

Cuando un cociente se eleva a un exponente, el resultado es el mismo cociente, pero con el dividendo y el divisor elevados al exponente dado. Matemáticamente, esto se representa como:

\[\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\]

Esta novena ley de los exponentes establece que cuando la base de una potencia es un cociente, tanto el numerador como el denominador se elevan al mismo exponente de la potencia.

Tabla de la ley de los exponentes

Ley de los exponentes	Expresión matemática
Potencia de exponente cero	a⁰=1
Potencia de exponente uno	a¹=a
Potencia de exponente negativo	a^-m=1/a^m
Potencia de exponente racional	a^m/n=√a^m
Multiplicación de potencias	a^m×aⁿ=a^m+n
División de potencias	a^m/aⁿ=a^m-n
Potencia de una potencia	(a^m)ⁿ=a^m×n
Potencia de un producto	(a×b)^m=a^m×b^m
Potencia de un cociente	(a/b)^m=a^m/b^m

Tabla de las leyes de los exponentes con ejemplos.

Tabla completa de las leyes de los exponentes

Para más información acerca del tema, puedes consultar Leyes de la potenciación del portal Serlo.