Dicciomat

Leyes de los radicales

Lista de todas las propiedades de los radicales

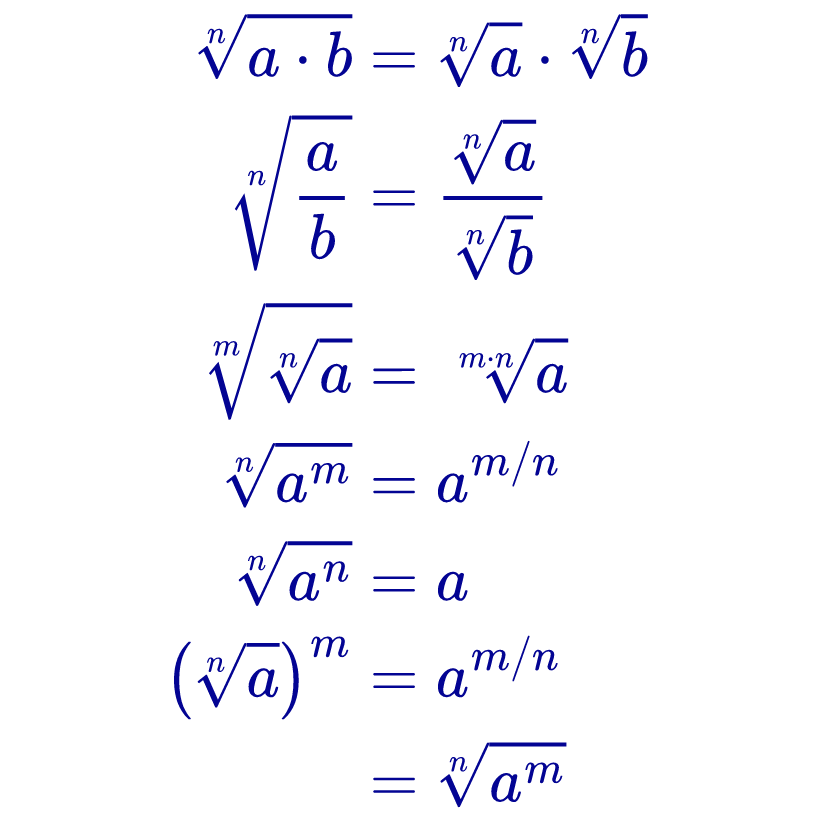
Las leyes de los radicales son reglas matemáticas que se utilizan para resolver y simplificar expresiones con radicales.

Estas leyes incluyen la raíz de un producto, la raíz de un cociente, la raíz de una raíz, la raíz de una potencia y la potencia de una raíz.

A continuación, se presentan a detalle en que consiste cada una de estas leyes junto con ejemplos que muestran su aplicación.

Tabla de contenido

Ley 1. Raíz de un producto

La raíz de índice “n” de un producto de dos factores es igual a la raíz de índice “n” del primer factor por la raíz de índice “n” del segundo factor.

Matemáticamente, la ley de la raíz de un producto se representa de la siguiente manera:

\[\sqrt[n]{a\cdot b}=\sqrt[n]{a}\cdot\sqrt[n]{b}\]

Esta ley establece que la raíz de un producto de factores es igual al producto de las raíces de los factores.

Por ejemplo, al aplicar la ley de la raíz de un producto para calcular la raíz cuadrada del producto 4·36, se obtiene lo siguiente:

\[\begin{aligned}\sqrt{4\cdot 36}&=\sqrt{4}\cdot\sqrt{36}\\&=2\cdot 6\\&=12\end{aligned}\]

De manera similar, de acuerdo con la ley de la raíz de un producto, la raíz cúbica del producto 8·64 es igual al producto de la raíz cúbica de 8 por la raíz cúbica de 64. Esto se expresa de la siguiente manera:

\[\begin{aligned}\sqrt[3]{8\cdot 64}&=\sqrt[3]{8}\cdot\sqrt[3]{64}\\&=2\cdot 4\\&=8\end{aligned}\]

Ley 2. Raíz de un cociente

La raíz de índice “n” de un cociente es igual a la raíz de índice “n” del dividendo entre la raíz de índice “n” del divisor.

Matemáticamente, la ley de la raíz de un cociente se expresa de la siguiente manera:

\[\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\]

Esta ley establece que la raíz de un cociente es igual al cociente de la raíz del dividendo entre la raíz del divisor.

Por ejemplo, considera el cociente 8/125. De acuerdo con la ley de la raíz de un cociente, al calcular la raíz cúbica del cociente 8/125, se obtiene lo siguiente:

\[\begin{aligned}\sqrt[3]{\frac{8}{125}}&=\frac{\sqrt[3]{8}}{\sqrt[3]{125}}\\&=\frac{2}{5}\end{aligned}\]

De manera similar, de acuerdo con la ley de la raíz de un cociente, la raíz cuadrada del cociente 81/100 es igual al cociente de la raíz cuadrada de 81 entre la raíz cuadrada de 100. Esto se expresa de la siguiente manera:

\[\begin{aligned}\sqrt{\frac{81}{100}}&=\frac{\sqrt{81}}{\sqrt{100}}\\&=\frac{9}{10}\end{aligned}\]

Ley 3. Raíz de una raíz

La raíz de índice “n” de una raíz de índice “m” de un número “a” es igual a la raíz de índice n·m del mismo radicando “a”.

Matemáticamente, la ley de la raíz de una raíz se expresa de la siguiente manera:

\[\sqrt[m]{\sqrt[n]{a}}=\sqrt[m\cdot n]{a}\]

Esta ley establece que la raíz de una raíz es igual a una raíz con el mismo radicando y cuyo índice es el producto de los índices originales.

Por ejemplo, de acuerdo con la ley de la raíz de una raíz, la raíz cúbica de la raíz cuadrada de 64 se calcula de la siguiente manera:

\[\begin{aligned}\sqrt[3]{\sqrt{64}}&=\sqrt[3\cdot 2]{64}\\&=\sqrt[6]{64}\\&=2\end{aligned}\]

De manera similar, de acuerdo con la ley de la raíz de una raíz, la raíz cuadrada de la raíz cuadrada de 16 es igual a la raíz cuarta de 16. Esto se expresa de la siguiente manera:

\[\begin{aligned}\sqrt{\sqrt{16}}&=\sqrt[2\cdot 2]{16}\\&=\sqrt[4]{16}\\&=2\end{aligned}\]

Ley 4. Raíz de una potencia

La raíz de índice “n” de una potencia de base “a” y exponente “m” es igual a una potencia con base “a” y exponente racional m/n.

Matemáticamente, la ley de la raíz de una potencia se expresa de la siguiente manera:

\[\sqrt[n]{a^m}=a^{m/n}\]

Esta ley establece que la raíz de una potencia es igual a una potencia con exponente racional, donde el numerador del número racional es el exponente de la potencia y el denominador es el índice de la raíz.

Por ejemplo, de acuerdo con la ley de la raíz de una potencia, la raíz cúbica de la potencia 49 es igual a 64, ya que:

\[\begin{aligned}\sqrt[3]{4^9}&=4^{\frac{9}{3}}\\&=4^3\\&=64\end{aligned}\]

La raíz de índice “n” de una potencia de base “a” y exponente “n” es igual a la base de la potencia. Matemáticamente, esto se expresa de la siguiente manera:

\[\sqrt[n]{a^n}=a^{n/n}=a\]

Esta propiedad se obtiene a partir de la ley de la raíz de una potencia y establece que, cuando el índice de la raíz es igual al exponente de la potencia, la raíz de la potencia es igual a la base de la potencia.

Por ejemplo, la raíz quinta de 25 es igual a 2, ya que, como el índice de la raíz es igual al exponente de la potencia, esta es igual a la base de la potencia. Esto se expresa de la siguiente manera:

\[\begin{aligned}\sqrt[5]{2^5}&=2^{\frac{5}{5}}\\&=2^1\\&=2\end{aligned}\]

Ley 5. Potencia de una raíz

Cuando una raíz de índice “n” de un número “a” se eleva a un exponente “m”, el resultado es igual a una potencia con base “a” y exponente racional m/n.

Matemáticamente, la ley de la potencia de una raíz se expresa de la siguiente manera:

\[\left(\sqrt[n]{a}\right)^m=a^{\frac{m}{n}}\]

Esta ley establece que, cuando la raíz de un número se eleva a un exponente, el resultado es igual a una potencia cuya base es el radicando y cuyo exponente es un número racional, donde el numerador es el exponente al que se elevó la raíz y el denominador es el índice de la raíz.

Como se puede observar, la ley de la potencia de una raíz y la ley de la raíz de una potencia son leyes equivalentes, ya que ambas resultan en la misma expresión, es decir:

\[\begin{aligned}\left(\sqrt[n]{a}\right)^m&=a^{\frac{m}{n}}\\&=\sqrt[n]{a^m}\end{aligned}\]

Para más información acerca del tema, consulta el artículo Leyes de los radicales del portal académico CCH UNAM.