Definición y partes de un logaritmo

Las partes de un logaritmo son la base y el argumento

El logaritmo en base “a” de un número “x” es igual a un número “y”, cuyo valor corresponde al valor del exponente al cual debe elevarse la base del logaritmo para obtener como resultado el número “x”.

La operación logaritmo sirve para calcular el valor del exponente al cual debe elevarse la base de una potencia para obtener como resultado un número específico.

Por ejemplo, ¿Cuál debe ser el valor del exponente para que una potencia de base 10 sea igual a 1000? En otras palabras, ¿Cuál debe ser el valor de “y” tal que 10^y=1000?

Si el logaritmo en base “a” de un número “x” es igual a un número “y”, entonces la base del logaritmo “a” elevada al exponente “y” dará como resultado el valor de “x”.

Por ejemplo, el logaritmo en base 10 de 1000 es igual a 3, ya que al elevar la base 10 al exponente 3 se obtiene como resultado 1000. Matemáticamente se cumple que:

\[\begin{aligned}10^3&=10\cdot 10\cdot 10\\&=100\cdot 10\\&=1000\end{aligned}\]

A continuación, veamos la definición formal y las partes de un logaritmo.

Tabla de contenido

Definición de logaritmo
Partes de un logaritmo
Ejemplos de logaritmos
Propiedades de los logaritmos

Definición de logaritmo

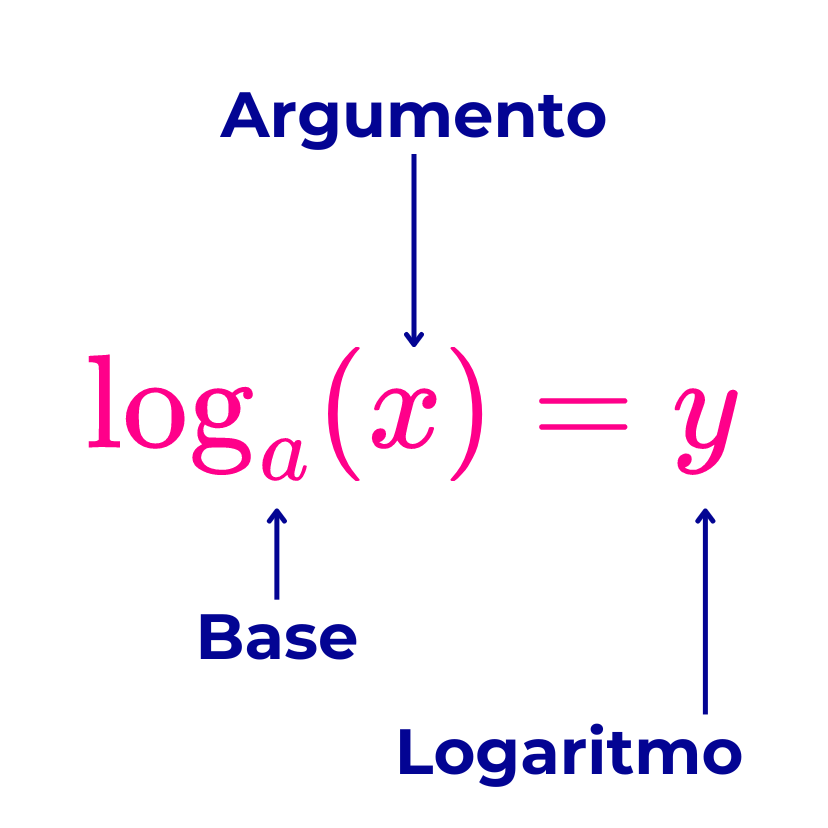
Dado un número real “x” mayor que cero y “a” un número real mayor que cero y diferente de uno, el logaritmo en base “a” de “x” se denota como log_a(x) y es igual a un número real “y” cuyo valor corresponde al valor del exponente al cual debe elevarse la base “a” del logaritmo para obtener como resultado el número “x”. Matemáticamente, esto se expresa de la siguiente manera:

\[\log_{a}(x)=y\Leftrightarrow a^y=x\]

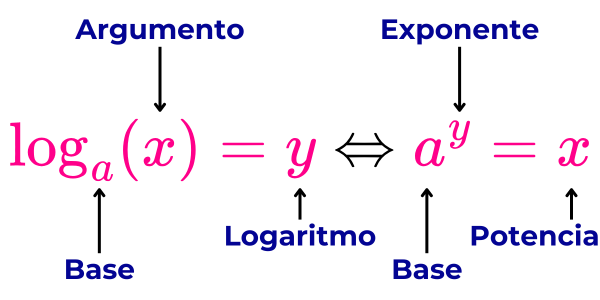
Esta expresión se lee como: El logaritmo en base “a” de “x” es igual a “y”, si y solo si “a” elevado al exponente “y” da como resultado “x”. Al tratarse de una doble implicación, se cumple que:

Si log_a(x)=y, entonces a^y=x.
Si a^y=x, entonces log_a(x)=y.

Partes de un logaritmo

Las partes de un logaritmo son la base, el argumento y el resultado o valor del logaritmo.

Base de un logaritmo: La base de un logaritmo es un número real mayor que cero y diferente de uno. En la expresión log_a(x)=y, “a” es la base del logaritmo.
Argumento de un logaritmo: El argumento de un logaritmo es un número real mayor que cero. En la expresión log_a(x)=y, “x” es el argumento del logaritmo.
Resultado o valor de un logaritmo: El resultado o valor del logaritmo es un número real menor que cero, igual a cero o mayor que cero. En la expresión log_a(x)=y, “y” corresponde al resultado del logaritmo.

Por ejemplo, en el logaritmo log₂(8)=3), la base es 2, el argumento es 8 y el resultado del logaritmo es 3.

Ejemplos de logaritmos

Para representar un logaritmo en una determinada base, primero se escribe la abreviatura "log", luego como subíndice la base del logaritmo y, por último, como argumento, el número cuyo logaritmo se desea calcular.

Por ejemplo, el logaritmo en base 5 de 625 se escribe como: log₅(625).

De acuerdo con la definición de logaritmo, este logaritmo es igual a 4, ya que la base del logaritmo, que es 5, elevada al exponente 4 da como resultado 625. Es decir:

\[\begin{aligned}5^4&=5\cdot 5\cdot 5\cdot 5\\&=25\cdot 5\cdot 5\\&=125\cdot 5\\&=625\end{aligned}\]

Por lo tanto, el logaritmo en base 5 de 625 es igual a 4, es decir: log₅(625)=4.

De manera similar, el logaritmo en base 2 de 1 se escribe como: log₂(1). Nuevamente, de acuerdo con la definición de logaritmo, este logaritmo es igual a cero, ya que la base del logaritmo, que es 2, elevada al exponente 0 da como resultado 1. Es decir:

\[2^0=1\]

Por lo tanto, el logaritmo en base 2 de 1 es igual a cero, es decir: log₂(1)=0.

Propiedades de los logaritmos

Los logaritmos tienen varias propiedades importantes que facilitan el cálculo y la simplificación de expresiones logarítmicas. Las propiedades de los logaritmos son:

Logaritmo de un producto: El logaritmo en base “a” de un producto es igual a la suma de los logaritmos en base “a” de los factores individuales:

\[\log_{a}(x\cdot y)=\log_{a}(x)+\log_{a}(y)\]

Logaritmo de un cociente: El logaritmo en base “a” de un cociente es igual a la diferencia entre el logaritmo en base “a” del numerador y el logaritmo en base “a” del denominador:

\[\log_{a}\left(\frac{x}{y}\right)=\log_{a}(x)-\log_{a}(y)\]

Logaritmo de una potencia: El logaritmo en base “a” de una potencia es igual al producto entre el exponente de la potencia y el logaritmo en base “a” de la base de la potencia:

\[\log_{a}(x^n)=n\cdot\log_{a}(x)\]

Logaritmo de una raíz: El logaritmo de una raíz es igual al producto entre el recíproco del índice de la raíz y el logaritmo del radicando:

\[\log_{a}(\sqrt[n]{x})=\frac{1}{n}\log_{a}(x)\]

Logaritmo de la base: El logaritmo en base “a” de “a” es igual a uno:

\[\log_{a}(a)=1\]

Logaritmo de uno: El logaritmo en base “a” de uno es igual a cero:

\[\log_{a}(1)=0\]

Para más información acerca del tema, puedes consultar "Logaritmos y sus propiedades" de la plataforma Superprof.