Dicciomat

Pendiente positiva, negativa, cero e indeterminada

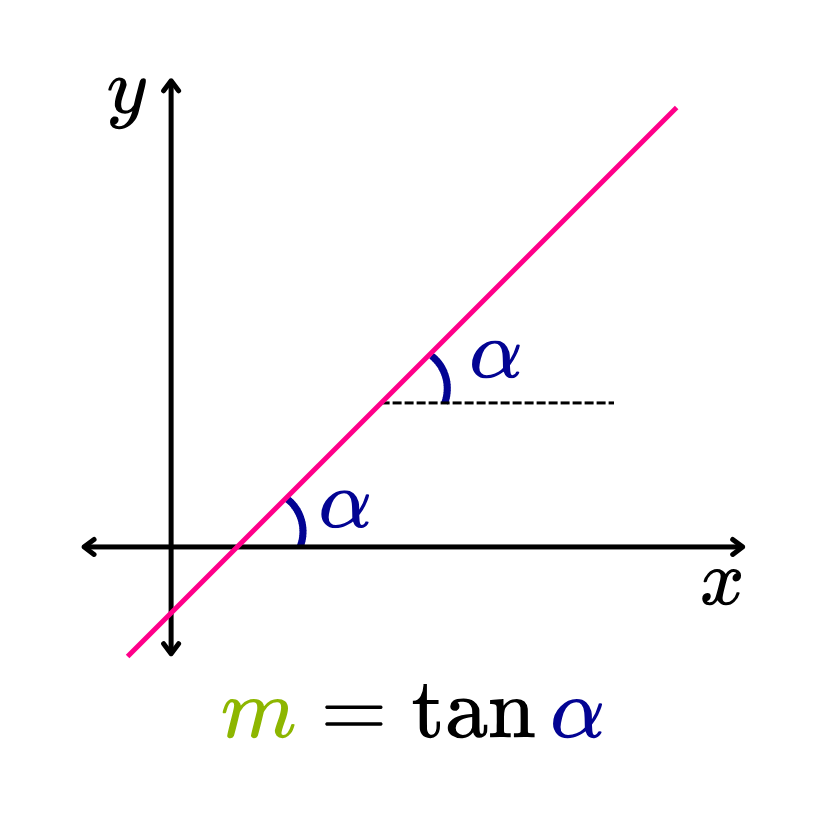
pendiente de una recta

La pendiente de una recta es la tangente del ángulo α que forma la recta con la dirección positiva del eje horizontal “x” en el plano cartesiano.

La pendiente de la recta se denota con la letra “m” y, matemáticamente, se expresa de la siguiente manera:

\[m=\tan(\alpha)\]
Tabla de contenido

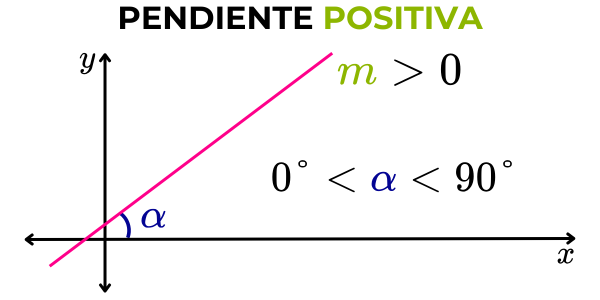
Pendiente positiva

Si el ángulo que forma la recta con la parte positiva del eje horizontal “x” es mayor que 0° y menor que 90° (ángulo agudo), entonces la pendiente de la recta es positiva. Cuando la pendiente de una recta es positiva, la recta va del tercer cuadrante hacia el primer cuadrante.

pendiente positiva

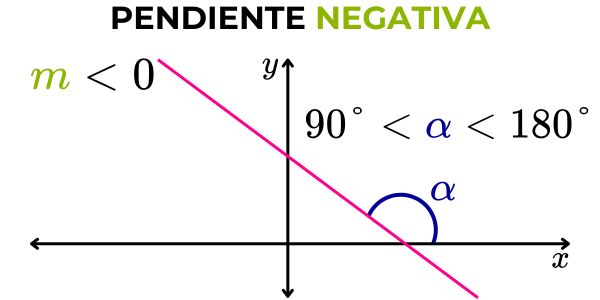
Pendiente negativa

Si el ángulo que forma la recta con la parte positiva del eje horizontal “x” es mayor que 90° y menor que 180° (ángulo obtuso), entonces la pendiente de la recta es negativa. Cuando la pendiente de una recta es negativa, la recta va del segundo cuadrante hacia el cuarto cuadrante.

pendiente negativa

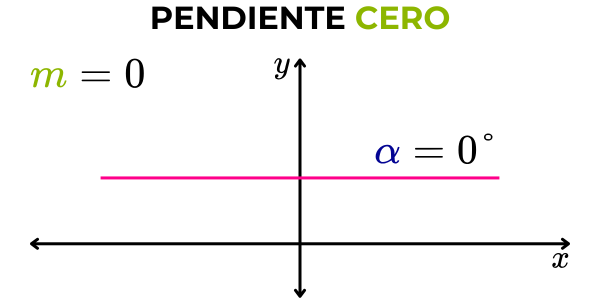
Pendiente cero

Si el ángulo que forma la recta con la parte positiva del eje horizontal “x” es igual a 0° (ángulo nulo), entonces la pendiente de la recta es igual a cero. Cuando la pendiente de una recta es igual a cero, la recta es una línea horizontal paralela al eje “x”.

pendiente cero

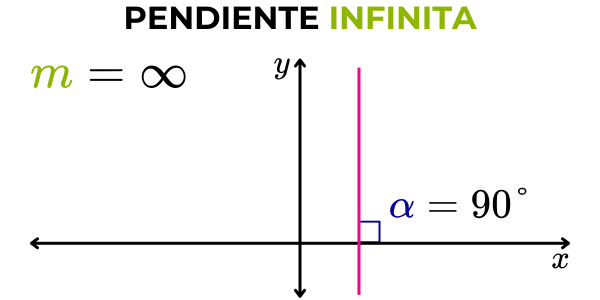
Pendiente indeterminada

Si el ángulo que forma la recta con la parte positiva del eje horizontal “x” es igual a 90° (ángulo recto), entonces la pendiente de la recta es indeterminada. Cuando la pendiente de una recta es indeterminada, la recta es una línea vertical paralela al eje “y”.

pendiente infinita

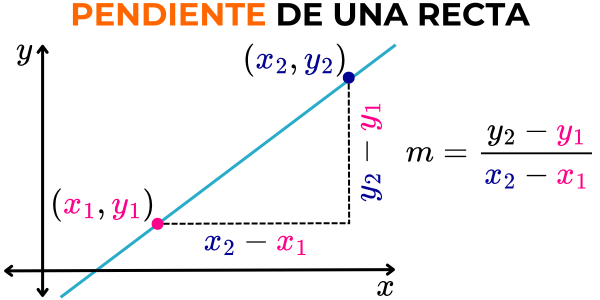
Pendiente de una recta que pasa por dos puntos

La fórmula para calcular la pendiente de una recta que pasa por dos puntos con coordenadas (x1, y1) y (x2, y2) se define como:

\[m=\frac{y_2-y_1}{x_2-x_1}\]
pendiente de una recta dados dos puntos

Pendiente de la recta que pasa por dos puntos ejemplos

Ejemplo 1. Determina la pendiente de la recta que pasa por los puntos A y B, cuyas coordenadas son (-1, 6) y (5, -4), respectivamente.

Solución: Dado que se conocen las coordenadas de dos puntos por los que pasa la recta, entonces se puede hallar la pendiente de la recta utilizando la fórmula definida para calcular la pendiente de la recta que pasa por dos puntos:

\[m=\frac{y_2-y_1}{x_2-x_1}\]

Para determinar la pendiente de la recta, simplemente se deben sustituir los valores de las coordenadas de los puntos en la fórmula. Para las coordenadas del punto A se tiene que x1=-1 y y1=6, y para el punto B se tiene que x2=5 y y2=-4. Al sustituir estos valores en la fórmula, se obtiene lo siguiente:

\[\begin{aligned}m&=\frac{y_2-y_1}{x_2-x_1}\\&=\frac{-4-6}{5-(-1)}\\&=\frac{-10}{5+1}\\&=\frac{-10}{6}\\&=-\frac{5}{3}\end{aligned}\]

Por lo tanto, la pendiente de la recta que pasa por los puntos (-1, 6) y (5, -4) es -5/3.

Ejemplo 2. Encuentra la pendiente de la recta que pasa a través de los puntos (-3, 17) y (4, 3).

Solución: Dado que se conocen las coordenadas de dos puntos por los que pasa la recta, se puede hallar la pendiente de la recta utilizando la fórmula para calcular la pendiente de la recta que pasa por dos puntos, la cual está definida como:

\[m=\frac{y_2-y_1}{x_2-x_1}\]

En este caso, las coordenadas (x1, y2) del primer punto son x1=-3 y y1=17, y las coordenadas del segundo punto (x2, y2) son x2=4 y y2=3. Al sustituir estos valores en la fórmula, se obtiene lo siguiente:

\[\begin{aligned}m&=\frac{y_2-y_1}{x_2-x_1}\\&=\frac{3-17}{4-(-3)}\\&=\frac{-14}{4+3}\\&=\frac{-14}{7}\\&=-\frac{14}{7}\\&=-2\end{aligned}\]

Por lo tanto, la pendiente de la recta que pasa a través de los puntos (-3, 17) y (4, 3) es -2.