Dicciomat

Producto cruz de vectores

producto cruz de dos vectores

El producto cruz de vectores, también conocido como producto vectorial, es una operación algebraica entre dos vectores que da como resultado un nuevo vector perpendicular a ambos vectores originales y, por lo tanto, normal al plano que los contiene.

El producto cruz de dos vectores se utiliza para determinar un vector perpendicular al plano generado por los vectores dados. Además, se utiliza para calcular áreas de paralelogramos y triángulos y tiene aplicaciones en diversos campos, tales como la física y la astronomía.

Tabla de contenido

Definición de producto cruz

Sean A y B dos vectores en un espacio tridimensional, definidos de la siguiente manera:

\[\begin{aligned}\vec{A}&= (a_1, a_2, a_3)\\\vec{B}&= (b_1, b_2, b_3)\end{aligned}\]

El producto cruz de estos vectores, se denota como A×B, se lee como "A cruz B" y es igual a un vector resultante C, que es perpendicular al plano formado por los vectores A y B.

La dirección y el sentido de este vector resultante C se determinan mediante la regla de la mano derecha.

Regla de la mano derecha

La regla de la mano derecha establece que, si los dedos de la mano derecha se curvan desde el primer vector hacia el segundo, el vector resultante apunta en la dirección en la que se extiende el dedo pulgar. Esto se representa en la siguiente imagen.

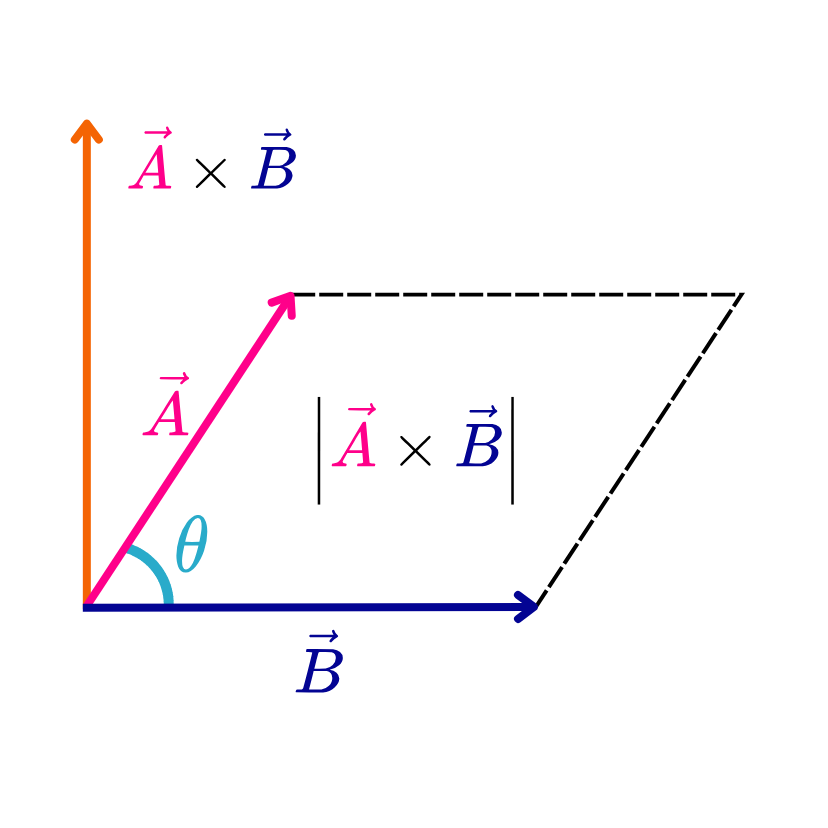
Magnitud del producto cruz

La magnitud del producto cruz es igual a la longitud del vector resultante. Es decir, si C es el vector resultante del producto cruz de los vectores A y B, su magnitud se define mediante la siguiente fórmula:

\[\begin{aligned}|\vec{C}|&=\left|\vec{A}\times\vec{B}\right|\\&=|\vec{A}||\vec{B}|\sin{\theta}\end{aligned}\]

En esta fórmula, |A| y |B| representan las longitudes de los vectores A y B, respectivamente, y θ es el ángulo entre estos vectores.

Área de un paralelogramo

Un paralelogramo es un cuadrilátero con dos pares de lados paralelos y opuestos. La siguiente imagen muestra un paralelogramo formado por los vectores A y B.

La fórmula para calcular el área de un paralelogramo se define como base por altura. En este caso, la base corresponde a la longitud del vector A, y la altura se obtiene como la longitud del vector B multiplicada por el seno del ángulo entre estos vectores A y B. Por lo tanto, el área del paralelogramo se expresa de la siguiente manera:

\[\text{Área}=|\vec{A}||\vec{B}|\sin{\theta}\]

Esto demuestra que el área de un paralelogramo es precisamente la magnitud del producto cruz de los vectores que lo forman.

Producto cruz de vectores usando sus componentes

Sean A y B dos vectores en tres dimensiones definidos como:

\[\begin{aligned}\vec{A}&=\left(a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k}\right)\\\vec{B}&=\left(b_{1}\vec{i}+b_{2}\vec{j}+b_{3}\vec{k}\right)\end{aligned}\]

El producto cruz de estos vectores se calcula mediante el siguiente determinante:

\[\begin{aligned}\vec{A}\times\vec{B}&=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\a_{1}&a_{2}&a_{3}\\b_{1}&b_{2}&b_{3}\end{vmatrix}\\\\&=\begin{vmatrix}a_{2}&a_{3}\\b_{2}&b_{3}\end{vmatrix}\vec{i}-\begin{vmatrix}a_{1}&a_{3}\\b_{1}&b_{3}\end{vmatrix}\vec{j}+\begin{vmatrix}a_{1}&a_{2}\\b_{1}&b_{2}\end{vmatrix}\vec{k}\end{aligned}\]

Propiedades del producto cruz

Sean A, B y C tres vectores y sea “m” un escalar. El producto cruz cumple las siguientes propiedades:

  • Propiedad anticonmutativa
  • Propiedad distributiva
  • Producto cruz de vectores paralelos
  • Producto cruz de un vector consigo mismo
  • Ortogonalidad del vector resultante

Propiedad anticonmutativa

La propiedad anticonmutativa del producto cruz establece que, al permutar los vectores, el vector resultante cambia de signo. Matemáticamente, se expresa de la siguiente manera:

\[\vec{A}\times\vec{B}=-\left(\vec{B}\times\vec{A}\right)\]

Propiedad distributiva

La propiedad distributiva del producto cruz con respecto a la suma de vectores establece que el producto cruz entre un vector y la suma de dos vectores es igual a la suma de los productos cruz de dicho vector con cada uno de los sumandos. Matemáticamente, se expresa de la siguiente manera:

\[\vec{A}\times\left(\vec{B}+\vec{C}\right)=\vec{A}\times\vec{B}+\vec{A}\times\vec{C}\]

Producto cruz de vectores paralelos

El producto cruz de dos vectores paralelos es siempre el vector nulo. Es decir, si el producto cruz de dos vectores diferentes al vector nulo es igual al vector nulo, entonces los vectores son paralelos.

Producto cruz de un vector consigo mismo

El producto cruz de un vector consigo mismo siempre da como resultado el vector nulo. Matemáticamente, esto se expresa de la siguiente manera:

\[\vec{A}\times\vec{A}=\vec{0}\]

Ortogonalidad del vector resultante

El vector resultante del producto cruz es ortogonal (perpendicular) a los vectores originales. Esto significa que el producto punto entre el vector resultante y cada uno de los vectores originales es igual a cero. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\vec{A}\cdot\left(\vec{A}\times\vec{B}\right)&=0\\\vec{B}\cdot\left(\vec{A}\times\vec{B}\right)&=0\\\end{aligned}\]