Dicciomat

Producto punto de vectores

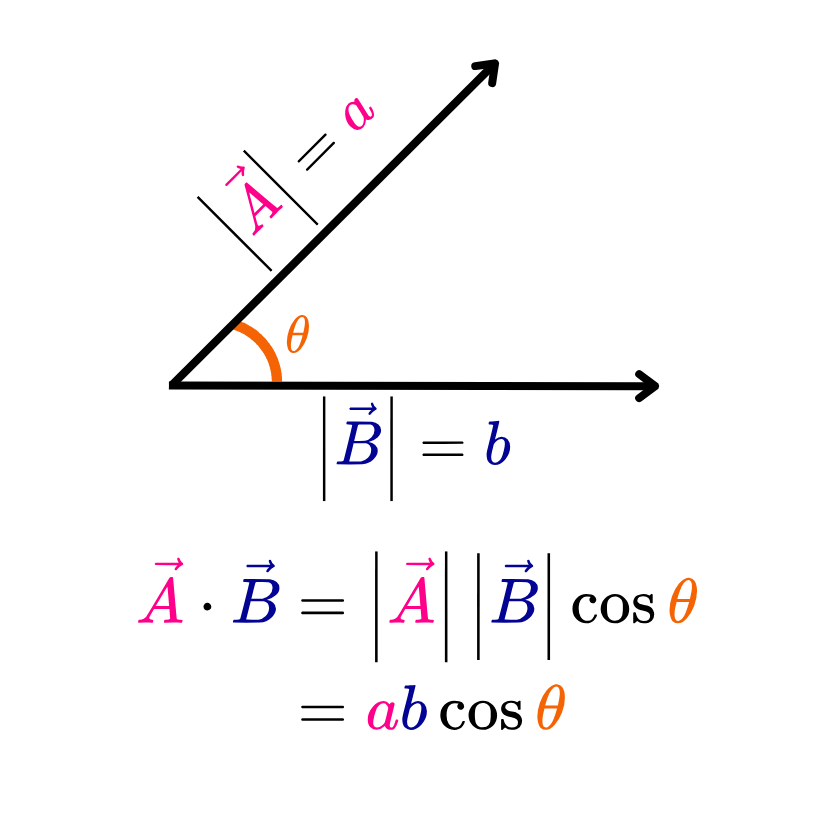
producto punto de dos vectores

El producto punto de vectores, también conocido como producto escalar o producto interno, es una operación algebraica entre vectores que da como resultado un escalar. Es decir, da como resultado un número real que puede ser positivo, negativo o cero.

Tabla de contenido

Definición de producto punto de vectores

Sean A y B dos vectores en un espacio euclidiano n-dimensional, definidos de la siguiente manera:

\[\begin{aligned}\vec{A}&=(a_1, a_2,\ldots, a_n)\\\vec{B}&=(b_1, b_2,\ldots, b_n)\end{aligned}\]

El producto punto de los vectores A y B se denota como:

\[\vec{A}\cdot\vec{B}\]

Se lee como "A punto B", y está definido como la suma de los productos de las componentes correspondientes de los dos vectores.

Matemáticamente, el producto punto de dos vectores en un espacio de “n” dimensiones se expresa de la siguiente manera:

\[\begin{aligned}\vec{A}\cdot\vec{B}&=a_1b_1+a_2b_2+\ldots +a_nb_n\\&=\sum_{i=1}^{n}a_ib_i\end{aligned}\]

Producto punto de vectores en dos dimensiones

Sean A y B dos vectores en un espacio euclidiano bidimensional definidos como:

\[\begin{aligned}\vec{A}&=(a_1, a_2)\\\vec{B}&=(b_1, b_2)\end{aligned}\]

El producto punto de dos vectores A y B en dos dimensiones está definido de la siguiente manera:

\[\vec{A}\cdot\vec{B}=a_1b_1+a_2b_2\]
fórmula del producto punto de dos vectores en dos dimensiones

Ejemplo 1. Calcula el producto punto de los vectores A y B definidos de la siguiente manera:

\[\begin{aligned}\vec{A}&=(2, 3)\\\vec{B}&=(5, 4)\end{aligned}\]

Solución: De acuerdo con la definición de producto punto de dos vectores en dos dimensiones, el producto punto es igual a la suma de los productos componente a componente. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\vec{A}\cdot\vec{B}&=(2, 3)\cdot (5, 4)\\&=(2)(5)+(3)(4)\\&=10+12\\&=22\end{aligned}\]

Por lo tanto, el producto punto de los vectores A y B es igual a 22.

Producto punto de vectores en tres dimensiones

Sean A y B dos vectores en un espacio euclidiano tridimensional definidos como:

\[\begin{aligned}\vec{A}&=(a_1, a_2, a_3)\\\vec{B}&=(b_1, b_2, b_3)\end{aligned}\]

El producto punto de dos vectores A y B en tres dimensiones está definido de la siguiente manera:

\[\vec{A}\cdot\vec{B}=a_1b_1+a_2b_2+a_3b_3\]
fórmula del producto punto de dos vectores en tres dimensiones

Ejemplo 2. Determina el producto punto de los vectores C y D definidos de la siguiente manera:

\[\begin{aligned}\vec{C}&=(3, 5, 2)\\\vec{D}&=(-1, 3, 0)\end{aligned}\]

Solución: Nuevamente, de acuerdo con la definición de producto punto de dos vectores en tres dimensiones, el producto punto es igual a la suma de los productos componente por componente. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\vec{C}\cdot \vec{D}&=(3, 5, 2)\cdot (-1, 3, 0)\\&=(3)(-1)+(5)(3)+(2)(0)\\&=-3+15+0\\&=12\end{aligned}\]

De esta manera, se obtiene que el producto punto de los vectores C y D es igual a 12.

Definición geométrica del producto punto de vectores

En términos geométricos, el producto punto de dos vectores es igual al producto de las magnitudes de los vectores por el coseno del ángulo entre ellos.

Sean A y B dos vectores en un espacio euclidiano n-dimensional, definidos como:

\[\begin{aligned}\vec{A}&=(a_1, a_2,\ldots, a_n)\\\vec{B}&=(b_1, b_2,\ldots, b_n)\end{aligned}\]

El producto punto de los vectores A y B se denota como:

\[\vec{A}\cdot\vec{B}\]

Se lee como "A punto B", y es igual al producto de la magnitud de cada vector por el coseno del ángulo θ entre ellos. Matemáticamente, si “a” es la magnitud del vector A, “b” es la magnitud del vector B, y θ es el ángulo entre los vectores A y B, entonces la fórmula para calcular el producto punto de vectores está definida de la siguiente manera:

\[\vec{A}\cdot\vec{B}=ab\cos{\theta}\]
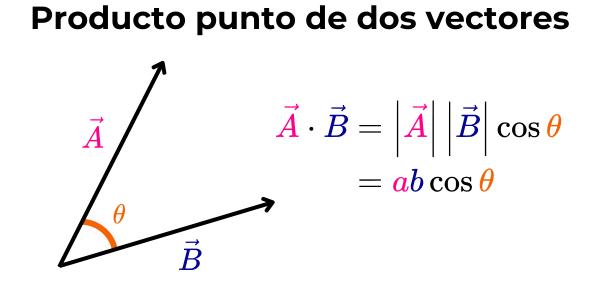
producto punto de dos vectores

Producto punto de vectores paralelos

Dos vectores son paralelos cuando el ángulo θ entre ellos es de 0° o 180°. En otras palabras, dos vectores son paralelos cuando tienen la misma dirección y el mismo sentido, o cuando tienen la misma dirección, pero sentido opuesto.

Dado que el coseno de 0° es igual a 1 y el coseno de 180° es igual a -1, entonces el producto punto entre dos vectores paralelos se reduce únicamente al producto de sus magnitudes.

Si el ángulo entre los vectores es de 0°, entonces el producto punto es igual al producto de las magnitudes de los vectores:

\[\begin{aligned}\vec{A}\cdot\vec{B}&=ab\cos{\theta}\\&=ab\cos(0°)\\&=ab(1)\\&=ab\end{aligned}\]

Si el ángulo entre los vectores es de 180°, entonces el producto punto es igual al producto de sus magnitudes, pero con signo negativo:

\[\begin{aligned}\vec{A}\cdot\vec{B}&=ab\cos{\theta}\\&=ab\cos(180°)\\&=ab(-1)\\&=-ab\end{aligned}\]

En resumen, cuando dos vectores son paralelos, el producto punto es igual al producto de sus magnitudes, con signo positivo si los vectores tienen el mismo sentido y con signo negativo si tienen sentido opuesto.

Producto punto de vectores perpendiculares

Dos vectores son perpendiculares cuando el ángulo entre ellos es de 90°.

Dado que el coseno de 90° es igual a cero, entonces el producto punto entre dos vectores perpendiculares es igual a cero:

\[\begin{aligned}\vec{A}\cdot\vec{B}&=ab\cos{\theta}\\&=ab\cos(90°)\\&=ab(0)\\&=0\end{aligned}\]

En resumen, cuando dos vectores son perpendiculares, su producto punto es igual a cero.

Propiedades del producto punto de vectores

Al igual que la suma y resta de vectores, el producto punto tiene algunas propiedades algebraicas fundamentales.

Sean A, B y C tres vectores en un espacio euclidiano n-dimensional, y “m” un escalar, el producto punto de vectores cumple las siguientes propiedades:

Propiedad conmutativa del producto punto

\[\vec{A}\cdot\vec{B}=\vec{B}\cdot\vec{A}\]

La propiedad conmutativa del producto punto establece que el orden en que se realice el producto punto no afecta el resultado, es decir, el producto punto es conmutativo. En otras palabras, el producto punto del vector A con el vector B es igual al producto punto del vector B con el vector A.

Propiedad distributiva del producto punto

\[\vec{A}\cdot\left(\vec{B}+\vec{C}\right)=\vec{A}\cdot\vec{B}+\vec{A}\cdot\vec{C}\]

La propiedad distributiva establece que el producto punto es distributivo con respecto a la suma de vectores. Es decir, el producto punto de un vector A con la suma de dos vectores B y C es igual a la suma de los productos punto de A con B y de A con C.

Propiedad asociativa al multiplicar el producto punto por un escalar

\[\begin{aligned}m\left(\vec{A}\cdot\vec{B}\right)&=\left(m\vec{A}\right)\cdot\vec{B}\\&=\vec{A}\cdot\left(m\vec{B}\right)\\&=\left(\vec{A}\cdot\vec{B}\right)m\end{aligned}\]

La propiedad asociativa establece que el producto punto es compatible con la multiplicación por un escalar. Esto significa que, si un escalar “m” multiplica a uno de los vectores involucrados en el producto punto, puede ser factorizado de diferentes maneras sin alterar el resultado.