Dicciomat

Propiedades de la integral indefinida

Lista completa de las propiedades de la integral indefinida

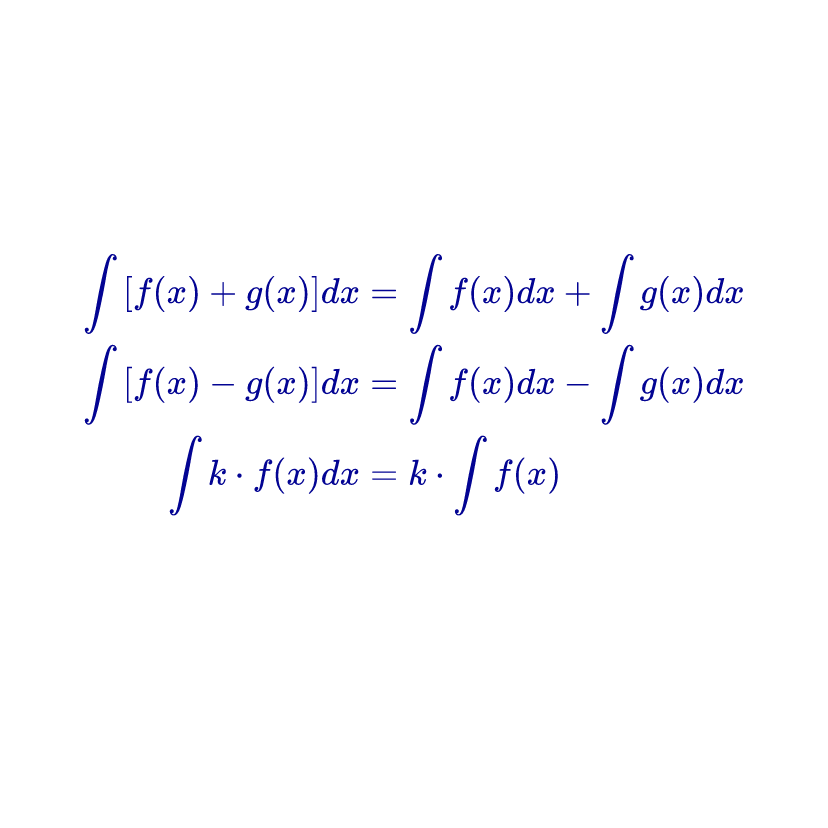
La integral indefinida de una función f(x) es el conjunto de las infinitas primitivas que puede tener dicha función f(x).

La integral indefinida de una función f(x) se expresa de la siguiente manera:

\[\int f(x)dx=F(x)+C\]

Las propiedades de la integral indefinida son reglas que permiten simplificar el cálculo de la integral indefinida de una función matemática. Estas propiedades son:

  • Integral indefinida de una suma de funciones.
  • Integral indefinida de una resta de funciones.
  • Integral indefinida del producto de una constante por una función.
propiedades de las integrales indefinidas

A continuación, veamos a detalle en qué consiste cada una de estas propiedades, así como algunos ejemplos de cómo aplicarlas para calcular la integral indefinida de una función.

Tabla de contenido

Propiedad 1. Integral indefinida de una suma de funciones

Dadas dos funciones f(x) y g(x), la integral indefinida de la suma de funciones f(x)+g(x) es igual a la integral indefinida de la función f(x) más la integral indefinida de la función g(x). Matemáticamente, esto se expresa de la siguiente manera:

\[\int [f(x)+g(x)]dx=\int f(x)dx+\int g(x)dx\]

Esta propiedad establece que la integral indefinida de una suma de dos funciones es igual a la suma de la integral indefinida de cada función.

Por ejemplo, sean f(x) y g(x) dos funciones definidas como f(x)=sin(x) y g(x)=cos(x). De acuerdo con la propiedad de la integral indefinida de una suma de funciones, la integral indefinida de f(x)+g(x) puede escribirse de la siguiente manera:

\[\int\left[\sin{(x)}+\cos{(x)}\right]dx=\int\sin{(x)}dx+\int\cos{(x)}dx\]

La propiedad de la integral indefinida de la suma de dos funciones puede aplicarse a una suma de más de dos funciones. Esto se expresa de la siguiente manera:

\[\begin{aligned}\int\left[f_{1}\left(x\right)+f_{2}\left(x\right)+...+f_{n}\left(x\right)\right]dx=\int f_{1}\left(x\right)dx+\int f_{2}\left(x\right)dx+...+\int f_{n}\left(x\right)dx\end{aligned}\]

Por ejemplo, considera la integral indefinida de x3+x2+x. De acuerdo con la propiedad de la integral indefinida de una suma, esta integral es igual a la suma de la integral indefinida de x3 más la integral indefinida de x2 más la integral indefinida de x. Matemáticamente, esto se expresa de la siguiente manera:

\[\int{\left(x^3+x^2+x\right)dx}=\int{x^3dx}+\int{x^2dx}+\int{xdx}\]

Propiedad 2. Integral indefinida de una resta de funciones

Dadas dos funciones f(x) y g(x), la integral indefinida de la resta de funciones f(x)-g(x) es igual a la integral indefinida de la función f(x) menos la integral indefinida de la función g(x). Matemáticamente, esto se expresa de la siguiente manera:

\[\int [f(x)-g(x)]dx=\int f(x)dx-\int g(x)dx\]

Esta propiedad establece que la integral indefinida de una resta de dos funciones es igual a la resta de la integral indefinida de cada función.

Por ejemplo, sean f(x) y g(x) dos funciones definidas como f(x)=cos(x) y g(x)=sin(x). De acuerdo con la propiedad de la integral indefinida de una resta de funciones, la integral indefinida de f(x)-g(x) puede escribirse de la siguiente manera:

\[\int\left(\cos{(x)}-\sin{(x)}\right)dx=\int\cos{(x)}dx-\int\sin{(x)}dx\]

La propiedad de la integral indefinida de una resta de funciones también puede aplicarse a una resta de más de dos funciones. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\int\left[f_{1}\left(x\right)-f_{2}\left(x\right)-...-f_{n}\left(x\right)\right]dx=\int f_{1}\left(x\right)dx-\int f_{2}\left(x\right)dx-...-\int f_{n}\left(x\right)dx\end{aligned}\]

Por ejemplo, considera la integral indefinida de x2-x-3. De acuerdo con la propiedad de la integral indefinida de una resta, esta integral puede escribirse como la integral indefinida de x2 menos la integral indefinida de x menos la integral indefinida de 3. Matemáticamente, esto se expresa de la siguiente manera:

\[\int{\left(x^2-x-3\right)dx}=\int{x^2dx}-\int{xdx}-\int{3dx}\]

Propiedad 3. Integral indefinida de una constante por una función

La integral indefinida del producto de una constante “k” por una función f(x) es igual a la constante “k” multiplicada por la integral indefinida de la función f(x). Matemáticamente, esto se expresa de la siguiente manera:

\[\int k\cdot f(x)dx=k\int f(x)dx\]

Esta propiedad establece que la integral indefinida del producto de una constante por una función es igual al producto de la constante por la integral indefinida de la función. En otras palabras, esta propiedad indica que un factor constante puede salir del símbolo de la integral.

Por ejemplo, sea “k” una constante cuyo valor es k=π y sea f(x) una función definida como f(x)=cos(x). De acuerdo con la propiedad de la integral indefinida de una constante por una función, la integral indefinida del producto π·cos(x) puede escribirse de la siguiente manera:

\[\int\pi\cdot\cos{(x)}dx=\pi\cdot\int\cos{(x)}\]

Videoclase sobre las propiedades de la integral indefinida

Preguntas frecuentes

¿Qué es una integral indefinida?

La integral indefinida de una función f(x) es el conjunto de las infinitas primitivas de la forma F(x)+C que puede tener la función f(x).

¿Cuáles son las propiedades de la integral indefinida?

Propiedad de linealidad: La integral indefinida de una suma o resta de funciones es igual a la suma o resta de las integrales indefinidas de esas funciones. Propiedad del factor constante: La integral indefinida del producto de una constante por una función es igual a la constante por la integral indefinida de la función.

¿Cómo se aplica la propiedad de linealidad en una integral indefinida?

La propiedad de linealidad permite descomponer la integral de una suma o resta de funciones en la suma o resta de las integrales de cada función por separado.

¿Cómo se calcula la integral indefinida de una función multiplicada por una constante?

De acuerdo con la propiedad del factor constante, la integral de una constante por una función es igual a la constante por la integral de la función.