Propiedades de la suma de vectores

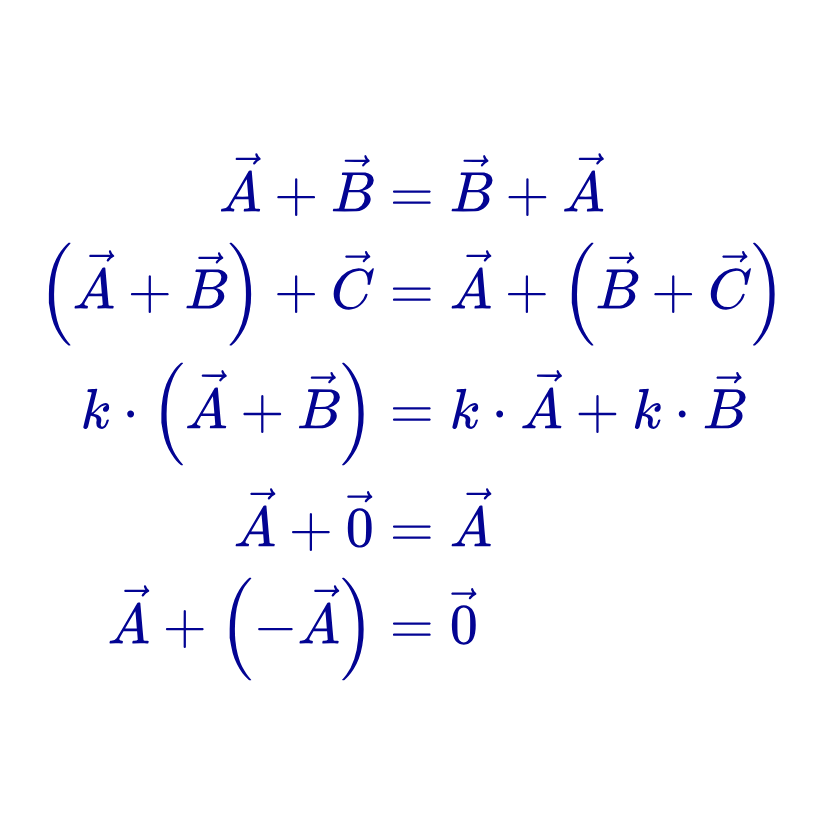
La suma de vectores es una operación matemática que permite combinar dos o más vectores individuales en un único vector, denominado vector suma o vector resultante. Existen dos métodos principales para realizar la suma de vectores: gráfica y analítica.

Propiedades de la suma de vectores

Las propiedades fundamentales de la suma de vectores son:

• Propiedad conmutativa
• Propiedad asociativa
• Propiedad distributiva
• Propiedad del elemento neutro
• Propiedad del elemento opuesto

A continuación, se describe a detalle cada una de estas propiedades.

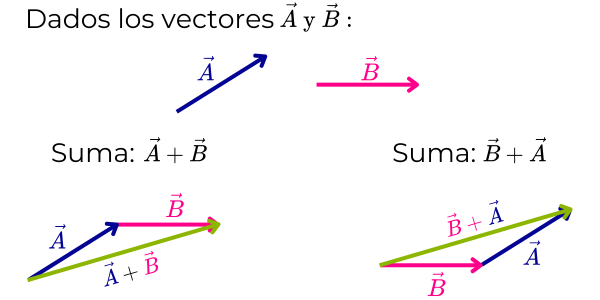
Propiedad conmutativa

La suma de vectores es conmutativa. Esta propiedad establece que el orden en el que se suman dos vectores no afecta el resultado. Matemáticamente, si A y B son dos vectores, entonces se cumple la siguiente igualdad:

Es decir, el vector resultante no cambia si se intercambia el orden de los vectores.

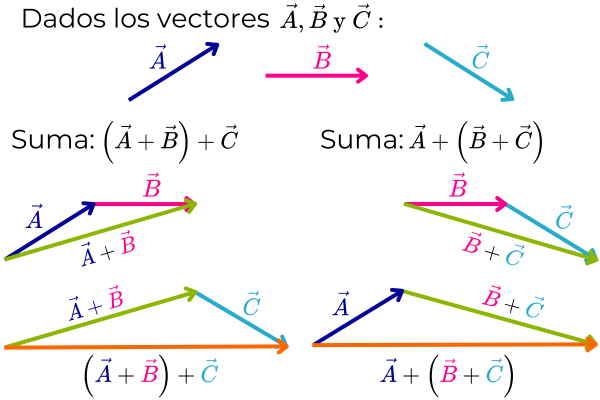
Propiedad asociativa

La suma de vectores es asociativa. Esta propiedad establece que la forma en la que se agrupan los vectores en una suma no afecta el resultado. Matemáticamente, si A, B y C son tres vectores, entonces se cumple la siguiente igualdad:

Esto significa que, al sumar tres o más vectores, pueden agruparse de cualquier manera y el vector resultante siempre será el mismo.

Propiedad distributiva respecto a la multiplicación por un escalar

La suma de vectores es distributiva con respecto a la multiplicación por un escalar. Esta propiedad establece que, si un escalar “k” multiplica una suma de vectores, este se distribuye a cada vector de la suma. Matemáticamente, si “k” es un escalar y A y B son dos vectores, entonces se cumple la siguiente igualdad:

Propiedad del elemento neutro o vector cero

La propiedad del elemento neutro establece que existe un vector denominado vector cero o vector nulo tal que, al sumarse con cualquier otro vector, se obtiene como resultado el mismo vector. Es decir, no altera el valor de ningún otro vector al sumarse. Matemáticamente, si A es un vector y 0 es el vector nulo, entonces se cumple la siguiente igualdad:

Propiedad del elemento opuesto

La propiedad del elemento opuesto establece que para cada vector A, existe un vector -A (vector opuesto) tal que, al sumarse, se obtiene como resultado el vector cero (vector nulo). Matemáticamente, esto se expresa de la siguiente manera:

El vector opuesto tiene la misma magnitud y dirección que el vector original, pero sentido contrario.

Preguntas frecuentes