Dicciomat

Propiedades de los límites

Lista completa de las propiedades de los límites.

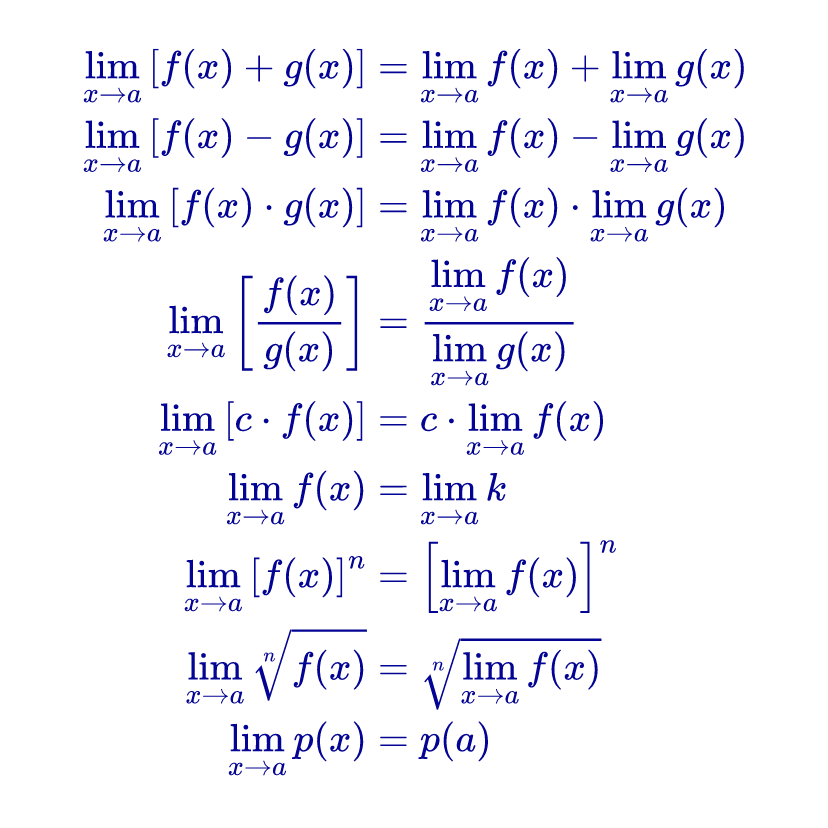
Las propiedades de los límites son reglas que se aplican para calcular el límite de una función.

Estas propiedades incluyen la propiedad del límite de una suma, una resta, una multiplicación y una división de funciones, además de la propiedad del límite de una función elevada a un exponente, el límite de la raíz enésima de una función y el límite de una función polinómica.

Tabla de contenido

Las propiedades de los límites

Sean f(x) y g(x) dos funciones definidas en un mismo intervalo, tales que existe el límite de ambas funciones cuando “x” se aproxima a un punto “a”:

\[\lim_{x\to a}f(x)=L\text{ y }\lim_{x\to a}g(x)=M\]

Si estos límites existen, entonces se cumplen cada una de las siguientes propiedades:

Propiedad 1. Límite de una suma

El límite de la suma de dos funciones en un punto es igual a la suma de los límites de cada función en ese mismo punto. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to a}\left[f(x)+g(x)\right]&=\lim\limits_{x\to a}f(x)+\lim\limits_{x\to a}g(x)\\&=L+M\end{aligned}\]

Esta propiedad establece que el límite de una suma es igual a la suma de los límites.

Por ejemplo, sean f(x) y g(x) dos funciones definidas como f(x)=3x y g(x)=x2. Para calcular el límite de la suma f(x)+g(x) cuando x→2, primero se calcula el límite cuando x→2 de la función f(x)=3x , luego se calcula el límite cuando x→2 de la función g(x)=x2 y, por último, se suman los valores obtenidos:

Para la función f(x), se obtiene lo siguiente:

\[\begin{aligned}\lim\limits_{x\to 2}f(x)&=\lim\limits_{x \to 2}(3x)\\&=3\cdot 2\\&=6\end{aligned}\]

Para la función g(x), se obtiene lo siguiente:

\[\begin{aligned}\lim\limits_{x\to 2}g(x)&=\lim\limits_{x\to 2}(x^2)\\&=2^2\\&=4\end{aligned}\]

De acuerdo con la propiedad del límite de una suma, el límite de la suma de dos funciones es igual a la suma de los límites de esas funciones, siempre que ambos límites existan. Por lo tanto, el límite cuando x→2 de la suma de funciones f(x)+g(x) queda definido de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to 2}\left[f(x)+g(x)\right]&=\lim\limits_{x\to 2}f(x)+\lim\limits_{x\to 2}g(x)\\&=\lim\limits_{x\to 2}3x+\lim\limits_{x\to 2}x^2\\&=6+4\\&=10\end{aligned}\]

Propiedad 2. Límite de una resta

El límite de la resta de dos funciones en un punto es igual a la resta de los límites de cada función en ese punto. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to a}\left[f(x)-g(x)\right]&=\lim\limits_{x\to a}f(x)-\lim\limits_{x\to a}g(x)\\&=L-M\end{aligned}\]

Esta propiedad establece que el límite de una resta es igual a la resta de los límites.

Por ejemplo, sean p(x) y q(x) dos funciones definidas como p(x)=x y q(x)=x3. Para calcular el límite de la resta de funciones p(x)-q(x) cuando x→4, primero se calcula el límite de p(x) cuando x→4, luego el límite de q(x) cuando x→4, y, por último, se restan los límites obtenidos.

Para la función p(x)=x, se obtiene lo siguiente:

\[\begin{aligned}\lim\limits_{x\to 4}p(x)&=\lim\limits_{x\to 4}x\\&=4\end{aligned}\]

Para la función q(x)=x3, se obtiene lo siguiente:

\[\begin{aligned}\lim\limits_{x\to 4}q(x)&=\lim\limits_{x\to 4}x^3\\&=4^3\\&=64\end{aligned}\]

Por lo tanto, el límite cuando x→4 de la resta de funciones p(x)-q(x) queda definido de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to 4}\left[p(x)-q(x)\right]&=\lim\limits_{x\to 4}p(x)-\lim\limits_{x\to 4}q(x)\\&=\lim\limits_{x\to 4}x-\lim\limits_{x\to 4}x^3\\&=4-64\\&=-60\end{aligned}\]

Propiedad 3. Límite de un producto

El límite del producto de dos funciones en un punto es igual al producto de los límites de cada función en ese punto. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to a}\left[f(x)\cdot g(x)\right]&=\lim\limits_{x\to a}f(x)\cdot\lim\limits_{x\to a}g(x)\\&=L\cdot M\end{aligned}\]

Esta propiedad establece que el límite de un producto es igual al producto de los límites.

Propiedad 4. Límite de un cociente

El límite de un cociente de funciones en un punto es igual al cociente de los límites de cada función en el mismo punto. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to a}\left[\frac{f(x)}{g(x)}\right]&=\frac{\lim\limits_{x\to a}f(x)}{\lim\limits_{x\to a}g(x)}\\&=\frac{L}{M}\end{aligned}\]

Esta propiedad establece que el límite de un cociente es igual al cociente de los límites, siempre que el límite del denominador sea diferente de cero.

Propiedad 5. Límite de una constante por una función

El límite del producto de una constante por una función en un punto es igual a la constante multiplicada por el límite de la función en el mismo punto. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to a}\left[c\cdot f(x)\right]&=c\cdot\lim\limits_{x\to a}f(x)\\&=c\cdot L\end{aligned}\]

Esta propiedad establece que el límite de una constante multiplicada por una función es igual a la constante multiplicada por el límite de la función. En otras palabras, un factor constante puede sacarse del signo del límite.

Propiedad 6. Límite de una función constante

Sea f(x) una función constante definida como f(x)=k, donde k es una constante. El límite de la función constante en un punto es igual a la misma constante. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to a}f(x)&=\lim\limits_{x\to a}k\\&=k\end{aligned}\]

Esta propiedad establece que el límite de una función constante es igual al valor constante de la función. En otras palabras, el límite de una función constante es la misma constante.

Propiedad 8. Límite de una función elevada a un exponente

El límite de una función elevada a un exponente “n” en un punto es igual al límite de la función en ese punto, elevado al mismo exponente “n”, donde “n” es un número entero positivo. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x\to a}\left[f(x)\right]^n&=\left[\lim\limits_{x\to a}f(x)\right]^n\\&=L^n\end{aligned}\]

Esta propiedad establece que el límite de una función elevada a un exponente es igual al límite de la función, elevado a dicho exponente.

Propiedad 9. Límite de la raíz enésima de una función

El límite de la raíz enésima de una función en un punto es igual a la raíz enésima del límite de la función en ese mismo punto. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\lim\limits_{x \to a}\sqrt[n]{f(x)}&=\sqrt[n]{\lim\limits_{x\to a}f(x)}\\&=\sqrt[n]{L}\end{aligned}\]

Esta propiedad establece que el límite de la raíz enésima de una función es igual a la raíz enésima del límite de la función.

Propiedad 10. Límite de una función polinómica

El límite de una función polinómica en un punto es igual al valor de la función en ese punto. Matemáticamente, esto se expresa de la siguiente manera:

\[\lim\limits_{x\to a}p(x)=p(a)\]

En esta expresión, p(x) es un polinomio. Esta propiedad establece que el límite de una función polinómica en un punto coincide con el valor de la función en ese mismo punto.

Por ejemplo, considera la función polinómica p(x) definida como p(x)=2x2-3x+1. De acuerdo con la propiedad del límite de una función polinómica, se cumple que:

\[\lim\limits_{x\to a}(2x^2-3x+1)=2a^2-3a+1\]

Es decir, el límite de la función p(x) cuando “x” se acerca al punto “a” es igual al valor de la función p(x) evaluada en “a”. Si por ejemplo a=2, entonces se obtiene que:

\[\begin{aligned}\lim\limits_{x\to 2}(2x^2-3x+1)&=2\cdot 2^2-3\cdot 2+1\\&=2\cdot 4-3\cdot 2+1\\&=8-6+1\\&=3\end{aligned}\]

Por lo tanto, el límite cuando “x” tiende a “2” de la función polinómica p(x)=2x2-3x+1 es igual a 3. Matemáticamente, esto se expresa de la siguiente manera:

\[\lim\limits_{x\to 2}2x^2-3x+1=3\]

Videoclase sobre las propiedades de los límites

Preguntas frecuentes sobre las propiedades de los límites

¿Cuáles son las propiedades de los límites?

Las propiedades de los límites son operaciones que se pueden emplear para simplificar el cálculo del límite de una función. Al tratarse de operaciones, también se les denomina álgebra de los límites o leyes de los límites.