Dicciomat

Propiedades de los logaritmos

Propiedades de los logaritmos

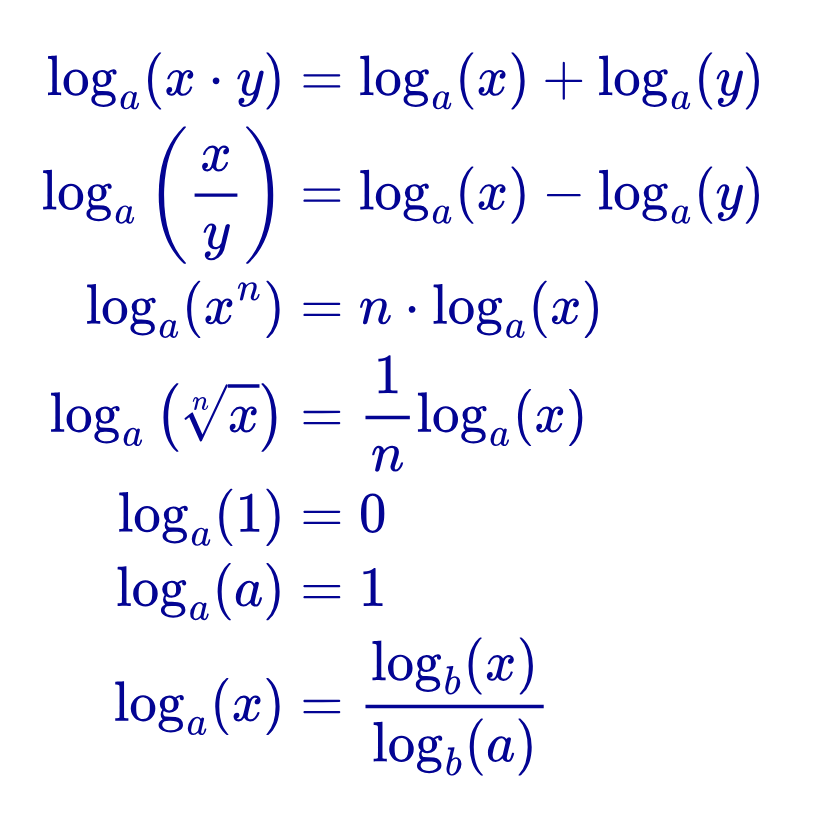
Las propiedades de los logaritmos son reglas que se utilizan para simplificar y resolver expresiones logarítmicas. Estas propiedades se deducen a partir de la definición de logaritmo y de las leyes de los exponentes.

A continuación, veamos cuáles son y en qué consisten cada una de las propiedades de los logaritmos, junto con algunos ejemplos de cómo se aplican para resolver y simplificar logaritmos.

Tabla de contenido

Propiedad del logaritmo de un producto

\[\log_{a}(x\cdot y)=\log_{a}(x)+\log_{a}(y)\]

La propiedad del logaritmo de un producto establece que el logaritmo de un producto es igual a la suma de los logaritmos de los factores individuales.

Por ejemplo, considera el logaritmo en base 2 de 18.

\[\log_2(18)\]

Este logaritmo puede reescribirse como un logaritmo en la misma base (base 2) del producto de los factores 2 y 9, es decir, puede reescribirse de la siguiente manera:

\[\log_2(18)=\log_2(2\cdot 9)\]

De acuerdo con la propiedad del logaritmo de un producto, cuando se tiene el logaritmo de un producto, este es igual a la suma de los logaritmos de los factores individuales.

Por lo tanto, el logaritmo en base 2 del producto de los factores 2 y 9 es igual al logaritmo en base 2 de 2 más el logaritmo en base 2 de 9. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\log_2(18)&=\log_2(2\cdot 9)\\&=\log_2(2)+\log_2(9)\end{aligned}\]

La propiedad del logaritmo de un producto también puede utilizarse para simplificar una suma de logaritmos cuando los logaritmos tienen la misma base.

Por ejemplo, considera la siguiente suma de logaritmos:

\[\log_{5}(25)+\log_{5}(4)\]

Dado que se trata de una suma de logaritmos con la misma base (base 5), entonces de acuerdo con la propiedad del logaritmo de un producto, esta suma es igual a un solo logaritmo en la misma base (base 5) del producto de los argumentos de los logaritmos. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\log_{5}(25)+\log_{5}(4)&=\log_{5}(25\cdot 4)\\&=\log_{5}(100)\end{aligned}\]

Propiedad del logaritmo de un cociente

\[\log_{a}\left(\frac{x}{y}\right)=\log_{a}(x)-\log_{a}(y)\]

La propiedad del logaritmo de un cociente establece que el logaritmo de un cociente es igual a la diferencia entre el logaritmo del dividendo y el logaritmo del divisor.

Por ejemplo, considera el logaritmo en base 3 del cociente 3/5.

\[\log_3\left(\frac{3}{5}\right)\]

De acuerdo con la propiedad del logaritmo de un cociente, este es igual a la diferencia entre el logaritmo del dividendo y el logaritmo del divisor. Así, el logaritmo en base 3 del cociente 3/5 es igual al logaritmo en base 3 de 3, menos el logaritmo en base 3 de 5. Matemáticamente, esto se expresa de la siguiente manera:

\[\log_{3}\left(\frac{3}{5}\right)=\log_{3}(3)-\log_{3}(5)\]

La propiedad del logaritmo de un cociente también se utiliza para simplificar una resta de logaritmos cuando estos tienen la misma base.

Por ejemplo, considera la siguiente resta de logaritmos:

\[\log_{3}(45)-\log_{3}(5)\]

Dado que se trata de una resta de logaritmos con la misma base (base 3), según la propiedad del logaritmo de un cociente, esta resta es igual a un solo logaritmo en la misma base (base 3) del cociente de los argumentos de los logaritmos. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\log_{3}(45)-\log_{3}(5)&=\log_{3}\left(\frac{45}{5}\right)\\&=\log_{3}(9)\end{aligned}\]

Propiedad del logaritmo de una potencia

\[\log_{a}(x^n)=n\cdot \log_{a}(x)\]

La propiedad del logaritmo de una potencia establece que el logaritmo de una potencia es igual al producto entre el exponente de la potencia y el logaritmo de la base de la potencia.

Por ejemplo, considera el logaritmo en base 2 de la potencia 43.

\[\log_2\left(4^3\right)\]

De acuerdo con la propiedad del logaritmo de una potencia, cuando se tiene el logaritmo de una potencia, este es igual al producto del exponente de dicha potencia por el logaritmo de su base. De este modo, el logaritmo en base 2 de 43 es igual al exponente 3 multiplicado por el logaritmo en base 2 de la base de la potencia 4. Matemáticamente, esto se expresa de la siguiente manera:

\[\log_{2}(4^3)=3\cdot\log_{2}(4)\]

La propiedad del logaritmo de una potencia también se utiliza para simplificar el producto entre un factor constante y un logaritmo. Por ejemplo, considera el siguiente producto:

\[2 \cdot \log_{4}(6)\]

Dado que se trata del producto de una constante por un logaritmo, de acuerdo con la propiedad del logaritmo de una potencia, esto es igual a un logaritmo en la misma base (base 4) y cuyo argumento es una potencia donde la base es el argumento del logaritmo original (6) y el exponente es el factor constante (2). Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}2 \cdot \log_{4}(6) &=\log_{4}(6^2)\\&=\log_{4}(36)\end{aligned}\]

Propiedad del logaritmo de una raíz

\[\log_{a}(\sqrt[n]{x})=\frac{1}{n}\log_{a}(x)\]

La propiedad del logaritmo de una raíz establece que el logaritmo de una raíz enésima es igual al producto entre el recíproco del índice de la raíz y el logaritmo del radicando.

Es importante destacar que esta propiedad es una extensión de la propiedad del logaritmo de una potencia, ya que, de acuerdo con las propiedades de los exponentes, la raíz enésima de un número real “x” es igual a una potencia de base “x” y exponente racional 1/n. Por lo tanto, la propiedad del logaritmo de una raíz puede escribirse de la siguiente manera:

\[\begin{aligned}\log_{a}(\sqrt[n]{x})&=\log_{a}(x^{1/n})\\&=\frac{1}{n}\log_{a}(x)\end{aligned}\]

Propiedad del logaritmo de uno

\[\log_{a}(1)=0\]

Esta propiedad establece que el logaritmo de 1 en cualquier base “a” es igual a cero. Por ejemplo, el logaritmo en base 3 de 1 es igual a cero. Matemáticamente, esto se expresa de la siguiente manera:

\[\log_{3}(1)=0\]

De manera similar, el logaritmo en base 7 de 1 es igual a cero, es decir:

\[\log_{7}(1)=0\]

Propiedad del logaritmo de la base

\[\log_{a}(a)=1\]

Esta propiedad establece que el logaritmo de la base, es decir, el logaritmo cuyo argumento es igual al valor de la base, es igual a uno.

Por ejemplo, el logaritmo en base 2 de 2 es igual a 1. Matemáticamente, esto se expresa de la siguiente manera:

\[\log_{2}(2)=1\]

De manera similar, el logaritmo en base 7 de 7 es igual a 1, es decir:

\[\log_{7}(7)=1\]

Lista completa de las propiedades de los logaritmos

Si "a" es un número real mayor que cero y distinto de uno, y tanto "x" como "y" son números reales positivos, mientras que "n" es un número real cualquiera, entonces se cumplen las siguientes propiedades de los logaritmos:

Logaritmo de un productologa(x⋅y)=loga(x)+loga(y)
Logaritmo de un cocienteloga(x/y)=loga(x)-loga(y)
Logaritmo de una potencialoga(xn)=n⋅loga(x)
Logaritmo de una raíz cuadradaloga(√x)=loga(x)/2
Logaritmo de unologa(1)=0
Logaritmo de la baseloga(a)=1
7 propiedades de los logaritmos