Propiedades del valor absoluto

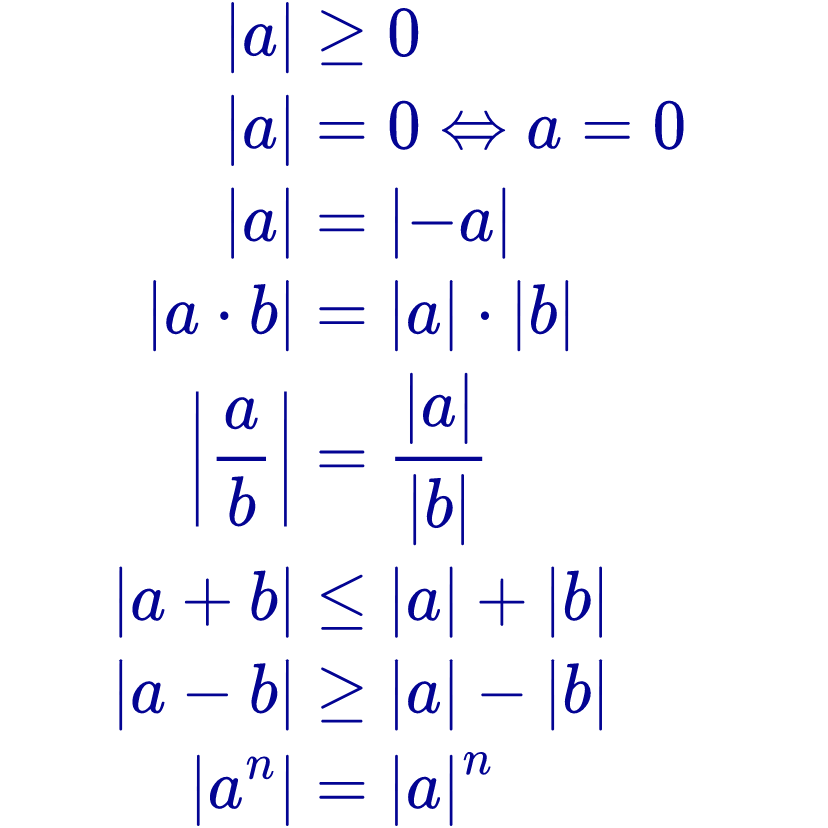
Las propiedades del valor absoluto son reglas matemáticas que describen cómo se comporta el valor absoluto cuando se aplican diversas operaciones algebraicas.

El valor absoluto de un número real “a”, ya sea positivo o negativo, se denota como |a| y es igual al mismo número “a”, pero con signo positivo.

Tabla de contenido

Definición formal de valor absoluto
Propiedades básicas del valor absoluto
Propiedades algebraicas del valor absoluto

Definición formal de valor absoluto

Definición del valor absoluto: Para cualquier número real “a”, el valor absoluto de “a” se denota como |a| y se define de la siguiente manera:

\[|a|=\left\{\begin{aligned}a&,\text{si}\ a\geq 0\\-a&,\text{si}\ a< 0\end{aligned}\right.\]

La definición de valor absoluto establece que:

Si “a” es un número mayor o igual a cero, entonces el valor absoluto de “a” es el mismo número “a”.
Si “a” es un número negativo, es decir, menor que cero, entonces el valor absoluto de “a” es el opuesto de “a”, es decir, es el valor de “a” multiplicado por -1.

Esto significa que el valor absoluto de un número positivo es igual al mismo número positivo. Por otra parte, el valor absoluto de un número negativo es igual al mismo número negativo, pero multiplicado por -1, lo cual lo vuelve un número positivo.

Por lo tanto, el valor absoluto de un número ya sea positivo o negativo, es siempre el mismo número, pero positivo.

Propiedades básicas del valor absoluto

Las propiedades básicas del valor absoluto se obtienen a partir de la definición de valor absoluto. Dados dos números reales “a” y “b”, se cumplen las siguientes propiedades:

Propiedad de la no negatividad del valor absoluto

El valor absoluto de un número real es no negativo. Esta propiedad establece que el valor absoluto de un número real “a”, ya sea positivo o negativo, es siempre positivo, es decir, es mayor que cero. Matemáticamente, esto se expresa de la siguiente manera:

\[|a|\geq 0\]

Propiedad del valor absoluto del número cero

El valor absoluto de un número real “a” es igual a cero, si y solo si “a” es igual a cero. Matemáticamente, esto se expresa de la siguiente manera:

\[|a|=0\Leftrightarrow a=0\]

Dado que se trata de una doble implicación, se cumplen las siguientes condicionales:

Si el valor absoluto de un número real “a” es igual a cero, entonces el número real “a” es igual a cero. Matemáticamente, esto se expresa de la siguiente manera: \[\text{Si }|a|=0\Rightarrow a=0\]
Si “a” es igual a cero, entonces el valor absoluto de cero es igual a cero. Matemáticamente, esto se expresa de la siguiente manera: \[\text{Si }a=0\Rightarrow |0|=0\]

Propiedad de simetría del valor absoluto

El valor absoluto de un número real “a” es igual al valor absoluto de su opuesto “-a”. Matemáticamente, esta propiedad establece que:

\[|a|=|-a|\]

Propiedad de la igualdad de valores absolutos

Los valores absolutos de dos números son iguales si y solo si los números son iguales o uno es el opuesto del otro. Matemáticamente, esto se expresa de la siguiente manera:

\[|a|=|b|\Leftrightarrow a=b\text{ o }a=-b\]

Como se trata de una doble implicación, se cumplen las siguientes condicionales:

Si los números “a” y “b” son iguales o “a” es el opuesto de “b”, entonces el valor absoluto de “a” es igual al valor absoluto de “b”.
Si el valor absoluto del número “a” es igual al valor absoluto del número “b”, entonces “a” es igual a “b” o “a” es el opuesto de “b”.

Propiedades algebraicas del valor absoluto

Las propiedades algebraicas del valor absoluto son un conjunto de reglas que establecen la relación del valor absoluto cuando se aplica a las operaciones básicas, tales como la suma, resta, multiplicación, división y potenciación.

Valor absoluto de un producto

El valor absoluto de un producto es igual al producto de los valores absolutos de los factores. Matemáticamente, esta propiedad establece que:

\[|a\cdot b|=|a|\cdot |b|\]

Valor absoluto de un cociente

El valor absoluto de un cociente es igual al cociente de los valores absolutos, siempre que el valor absoluto del divisor sea diferente de cero. Matemáticamente, esta propiedad establece que:

\[\left|\frac{a}{b}\right|=\frac{|a|}{|b|}\]

Valor absoluto de una suma: Desigualdad triangular

El valor absoluto de una suma de dos números es menor o igual que la suma de los valores absolutos de los sumandos. Matemáticamente, esta propiedad establece que:

\[|a+b|\leq |a|+|b|\]

La propiedad del valor absoluto de una suma se denomina desigualdad triangular.

Si “a” y “b” son diferentes de cero y ambos tienen el mismo signo, ya sea que ambos sean positivos o negativos, se cumple que el valor absoluto de la suma es igual a la suma de los valores absolutos de los sumandos. Matemáticamente, si “a” y “b” tienen signos iguales, entonces se cumple que:

\[|a+b|=|a|+|b|\]

Valor absoluto de una resta

El valor absoluto de una resta de dos números es mayor o igual que la resta del valor absoluto del minuendo menos el valor absoluto del sustraendo. Matemáticamente, esto se expresa de la siguiente manera:

\[|a-b|\geq |a|-|b|\]

Valor absoluto de una potencia

El valor absoluto de una potencia de base “a” y exponente “n” es igual a una potencia cuya base es el valor absoluto de “a” y exponente “n”. Matemáticamente, esta propiedad establece que:

\[\left|a^n\right|=\left|a\right|^n\]