Dicciomat

Punto medio de un segmento

punto medio de un segmento

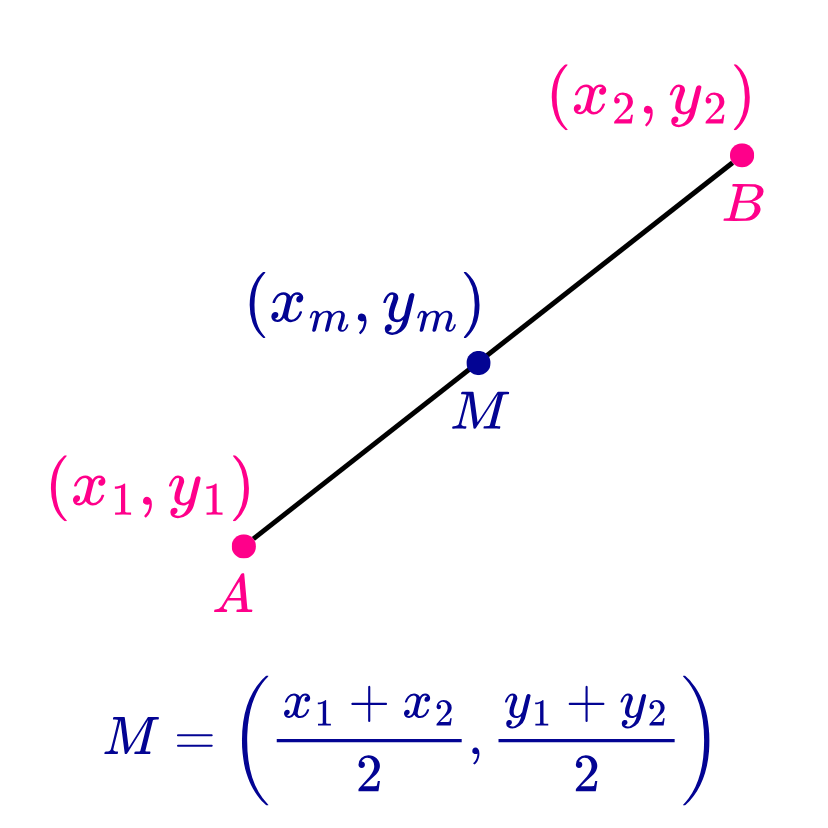
El punto medio de un segmento es un punto “M” con coordenadas (xm, ym) que se encuentra exactamente a la misma distancia de los extremos del segmento.

En otras palabras, el punto medio es aquel que divide al segmento en dos partes iguales.

Un segmento puede ubicarse en el plano o bien en el espacio tridimensional, por lo que la fórmula para hallar el punto medio varía según sea el caso.

Tabla de contenido

Fórmula para hallar el punto medio de un segmento en el plano

La fórmula para hallar el punto medio de un segmento se expresa a partir de las coordenadas de los extremos de dicho segmento.

Si el segmento de recta va desde un punto “A” con coordenadas (x1, y1) hasta un punto “B” con coordenadas (x2, y2), entonces las coordenadas (xm, ym) del punto medio “M” se calculan de la siguiente manera:

La coordenada horizontal xm del punto medio es igual a la mitad de la suma de las coordenadas en “x” de los extremos. Matemáticamente, esto se expresa de la siguiente manera:

\[x_m=\frac{x_1+x_2}{2}\]

La coordenada vertical ym del punto medio es igual a la mitad de la suma de las coordenadas en “y” de los extremos. Matemáticamente, esto se expresa de la siguiente manera:

\[y_m=\frac{y_1+y_2}{2}\]

Por lo tanto, las coordenadas (xm, ym) del punto medio “M” quedan definidas de la siguiente manera:

\[(x_m, y_m)=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\]

Dado que ahora se tiene una expresión para las coordenadas del punto medio, entonces la fórmula para hallar el punto medio de un segmento en el plano cartesiano está definida de la siguiente manera:

\[\begin{aligned}M&=(x_m, y_m)\\&=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\end{aligned}\]
formula del punto medio de un segmento

Fórmula para hallar el punto medio de un segmento en el espacio tridimensional

La fórmula para calcular el punto medio de un segmento en el espacio tridimensional se expresa a partir de las coordenadas de los extremos del segmento.

Si el segmento de recta va desde un punto “A” con coordenadas (x1, y1, z1) hasta un punto “B” con coordenadas (x2, y2, z2), entonces las coordenadas del punto medio “M” se calculan de la siguiente manera:

La coordenada en “x” del punto medio es igual a la mitad de la suma de las coordenadas en “x” de los extremos. Matemáticamente, esto se expresa de la siguiente manera:

\[x_m=\frac{x_1 + x_2}{2}\]

La coordenada en “y” del punto medio es igual a la mitad de la suma de las coordenadas en “y” de los extremos. Matemáticamente, se expresa de la siguiente manera:

\[y_m=\frac{y_1+y_2}{2}\]

La coordenada en “z” del punto medio es igual a la mitad de la suma de las coordenadas en “z” de los extremos. Matemáticamente, se expresa de la siguiente manera:

\[z_m=\frac{z_1+z_2}{2}\]

Por lo tanto, las coordenadas (xm, ym, zm) del punto medio “M” de un segmento en el espacio tridimensional están definidos de la siguiente manera:

\[(x_m, y_m, z_m)=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}, \frac{z_1+z_2}{2}\right)\]

Coordenadas del punto medio

Las coordenadas (xm, ym) del punto medio “M” de un segmento que va desde un punto “A” con coordenadas (x1, y1) hasta un punto “B” con coordenadas (x2, y2) están definidas de la siguiente manera:

\[x_m=\frac{x_1+x_2}{2}, \quad y_m=\frac{y_1+y_2}{2}\]

Para hallar estas coordenadas, es necesario conocer las coordenadas de los extremos del segmento.

Por ejemplo, para hallar las coordenadas del punto medio de un segmento que va del punto “A” de coordenadas (2, 5) hacia el punto “B” de coordenadas (6, 9), primero se identifican los valores de las coordenadas en “x” y en “y” y luego se sustituyen sus valores en las fórmulas de las coordenadas del punto medio de un segmento.

Por un lado, se tiene que x1=2 y x2=6. De tal manera que, la coordenada en “x” del punto medio está definida de la siguiente manera:

\[\begin{aligned}x_m&=\frac{x_1+x_2}{2}\\&=\frac{2+6}{2}\\&=\frac{8}{2}\\&=4\end{aligned}\]

Por otro lado, se tiene que y1=5 y y2=9. De tal manera que, la coordenada en “y” del punto medio está definida de la siguiente manera:

\[\begin{aligned}y_m&=\frac{y_1+y_2}{2}\\&=\frac{5+9}{2}\\&=\frac{14}{2}\\&=7\end{aligned}\]

Por lo tanto, las coordenadas (xm, ym) del punto medio m de un segmento que va desde el punto “A” con coordenadas (2, 5) hasta el punto “B” con coordenadas (6, 9) son (9, 7).

Punto medio entre dos puntos

Para hallar el punto medio entre dos puntos “A” y “B” con coordenadas (x1, y1) y (x2, y2), respectivamente, simplemente se sustituyen los valores de las coordenadas en la fórmula:

\[\begin{aligned}M&=(x_m, y_m)\\&=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\end{aligned}\]

Por ejemplo, para hallar el punto medio entre dos puntos “A” y “B” de coordenadas (3, 9) y (-1, 5), respectivamente, se sustituyen los valores de las coordenadas en la fórmula anterior.

En este caso se tiene que x1=3, y1=9, x2=-1 y y2=5. Al sustituir estos valores en la fórmula para hallar el punto medio de un segmento, se obtiene lo siguiente:

\[\begin{aligned}M&=(x_m, y_m)\\&=\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\\&=\left(\frac{3+(-1)}{2},\frac{9+5}{2}\right)\\&= \left(\frac{3-1}{2},\frac{9+5}{2}\right)\\&=\left(\frac{2}{2},\frac{14}{2}\right)\\&=(1, 7)\end{aligned}\]

Por lo tanto, el punto medio entre los puntos (3, 9) y (-1, 5) es el punto (1, 7).

Preguntas frecuentes

¿Cómo hallar las coordenadas del punto medio de un segmento?

La coordenada en “x” del punto medio es igual a la mitad de la suma de las coordenadas en “x” de los extremos. De forma similar, la coordenada en “y” del punto medio es igual a la mitad de la suma de las coordenadas en “y” de los extremos.

¿Cuáles son las coordenadas del punto medio de un segmento?

Las coordenadas del punto medio “M” de un segmento en el plano son (xm, ym), las cuales están definidas como x_m=(x1+x2)/2 y y_m=(y1+y2)/2.

¿Cómo determinar las coordenadas del punto medio de un segmento?

Para determinar las coordenadas del punto medio de un segmento, es necesario conocer las coordenadas de los extremos del segmento. Si un segmento va desde un punto “A” con coordenadas (x1, y1) hasta un punto “B” con coordenadas (x2, y2), las coordenadas del punto medio “M” están definidas como: xm=(x1+x2)/2 y ym=(y1+y2)/2.