Razones trigonométricas de un triángulo rectángulo

Las razones trigonométricas de un triángulo rectángulo son las relaciones entre las longitudes de sus lados en función de uno de sus ángulos agudos.
Las principales razones trigonométricas son el seno (sin), el coseno (cos) y la tangente (tan), las cuales se definen de la siguiente manera:
El seno de un ángulo agudo α es la razón entre la longitud del cateto opuesto al ángulo α y la longitud de la hipotenusa. Esta razón se expresa de la siguiente manera:
El coseno de un ángulo agudo α es la razón entre la longitud del cateto adyacente al ángulo α y la longitud de la hipotenusa. Esta razón se expresa de la siguiente manera:
La tangente de un ángulo agudo α es la razón entre la longitud del cateto opuesto y la longitud del cateto adyacente. Esta razón se expresa de la siguiente manera:
Triángulo rectángulo
Un triángulo rectángulo es un tipo de triángulo que tiene un ángulo recto (ángulo de 90 grados) y dos ángulos agudos (ángulos mayores que 0 grados y menores de 90 grados).
Los dos lados que forman el ángulo recto se denominan catetos. En particular, se denominan "cateto adyacente" y "cateto opuesto" en relación con alguno de los dos ángulos agudos.
El lado opuesto al ángulo recto se denomina hipotenusa y es el lado de mayor longitud del triángulo rectángulo.
La siguiente imagen muestra las características de un triángulo rectángulo.
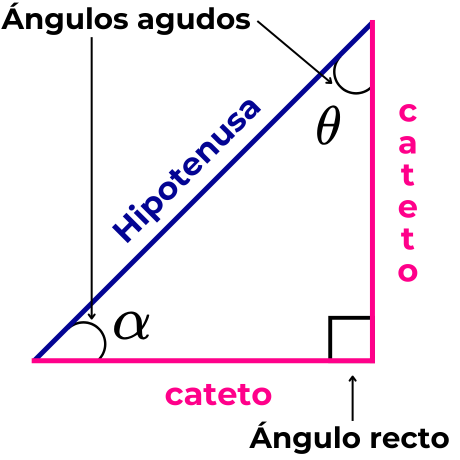
Cateto adyacente en un triángulo rectángulo
El cateto adyacente a un ángulo agudo en un triángulo rectángulo es el lado que, junto con la hipotenusa, forma dicho ángulo.
En la siguiente imagen se muestra un triángulo rectángulo cuyas longitudes de los catetos (los lados que forman el ángulo recto) son A y B, y donde C representa la longitud de la hipotenusa.
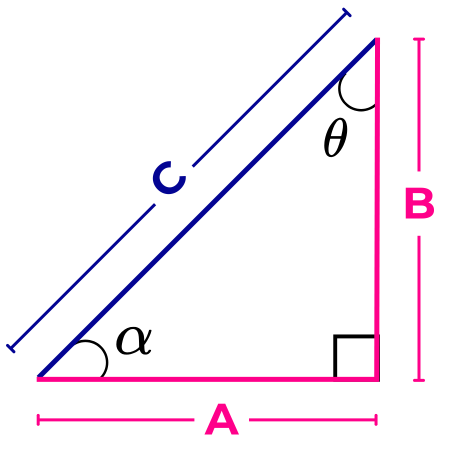
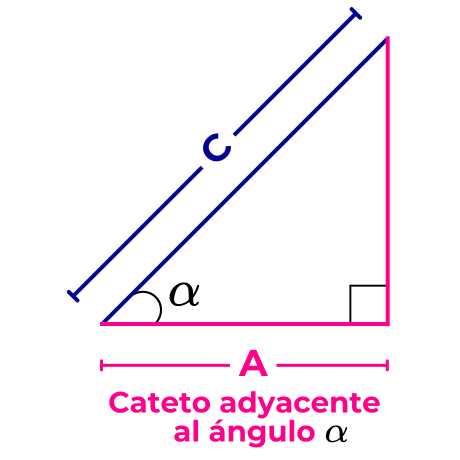
El cateto adyacente al ángulo α es el lado de longitud A, ya que este, junto con la hipotenusa, forma el ángulo α.
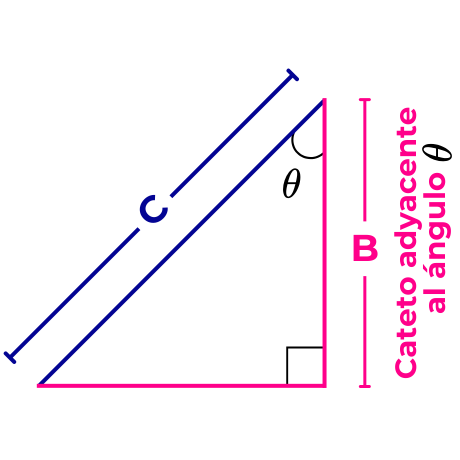
El cateto adyacente al ángulo θ es el lado de longitud B, ya que este, junto con la hipotenusa, forma el ángulo θ.
Cateto opuesto en un triángulo rectángulo
El cateto opuesto a un ángulo agudo es uno de los lados del triángulo rectángulo que no forman dicho ángulo. El cateto opuesto a un ángulo agudo puede interpretarse como el lado del triángulo que se encuentra frente a ese ángulo.
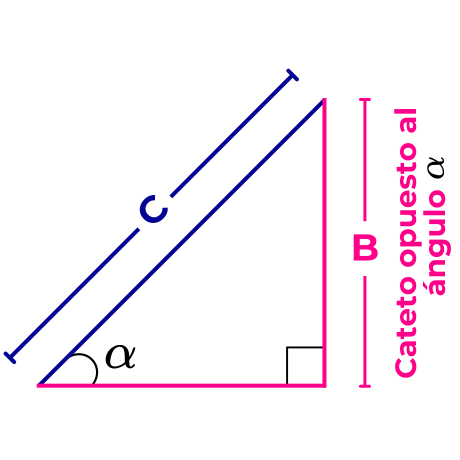
En la siguiente imagen se muestra un triángulo rectángulo cuyas longitudes de los catetos (los lados que forman el ángulo recto) son A y B, y C representa la longitud de la hipotenusa.
El cateto opuesto al ángulo α es el lado de longitud B, ya que no forma el ángulo α y se encuentra frente a este ángulo α.
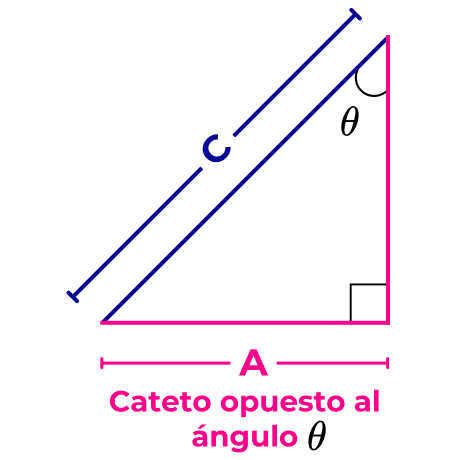
El cateto opuesto al ángulo θ es el lado de longitud A, ya que este no forma el ángulo θ y se encuentra frente a este ángulo θ.
Razones trigonométricas
Las razones trigonométricas son relaciones matemáticas que se establecen entre los lados de un triángulo rectángulo en función de cada uno de sus dos ángulos agudos. A continuación, se define a detalle la razón trigonométrica seno, coseno y tangente.
Seno de un ángulo
En un triángulo rectángulo, el seno de un ángulo agudo es la razón entre la longitud del cateto opuesto a dicho ángulo y la longitud de la hipotenusa.
Si en un triángulo rectángulo los ángulos agudos se representan por α y θ, entonces el seno del ángulo α es la razón entre la longitud del cateto opuesto al ángulo α y la longitud de la hipotenusa. Se denota como sin(α) y se expresa de la siguiente manera:
De manera similar, el seno del ángulo θ se define como la razón entre la longitud del cateto opuesto al ángulo θ y la longitud de la hipotenusa. Se denota como sin(θ) y se expresa de la siguiente forma:
Es importante destacar que la razón trigonométrica seno se define de la misma manera para ambos ángulos agudos α y θ. Sin embargo, el valor resultante es diferente para cada ángulo, ya que este depende de las longitudes de los catetos y de la longitud de la hipotenusa.
La siguiente imagen muestra un triángulo rectángulo en el que A y B representan las longitudes de los catetos (lados que forman el ángulo recto) y C representa la longitud de la hipotenusa.
La razón trigonométrica seno para el ángulo α está definida de la siguiente manera:
La razón trigonométrica seno para el ángulo θ está definida de la siguiente manera:
Coseno de un ángulo
El coseno de un ángulo agudo es la razón entre la longitud del cateto adyacente a dicho ángulo y la longitud de la hipotenusa.
Si en un triángulo rectángulo los ángulos agudos se representan por α y θ, entonces el coseno del ángulo α es la razón entre la longitud del cateto adyacente al ángulo α y la longitud de la hipotenusa. Se denota como cos(α) y se expresa matemáticamente de la siguiente manera:
De manera similar, el coseno del ángulo θ se define como la razón entre la longitud del cateto adyacente al ángulo θ y la longitud de la hipotenusa. Se denota como cos(θ) y se expresa matemáticamente de la siguiente forma:
De la misma manera que con la razón seno, es importante destacar que la razón trigonométrica coseno se define de la misma forma para ambos ángulos agudos α y θ. Sin embargo, el valor resultante es diferente para cada ángulo, ya que este depende de las longitudes de los catetos y de la hipotenusa.
Tomando como referencia la imagen anterior, en la que A y B representan las longitudes de los catetos (lados que forman el ángulo recto) y C representa la longitud de la hipotenusa, la razón trigonométrica coseno para el ángulo α está definida de la siguiente manera:
Por otro lado, la razón trigonométrica coseno para el ángulo θ está definida de la siguiente manera:
Tangente de un ángulo
La tangente de un ángulo agudo es la razón entre la longitud del cateto opuesto y la longitud del cateto adyacente.
Si en un triángulo rectángulo sus dos ángulos agudos se representan por α y θ, entonces la tangente del ángulo α es la razón entre la longitud del cateto opuesto al ángulo α y la longitud del cateto adyacente al ángulo α. Se denota como tan(α) y se expresa matemáticamente de la siguiente manera:
De manera similar, la tangente del ángulo θ se define como la razón entre la longitud del cateto opuesto al ángulo θ y la longitud del cateto adyacente al ángulo θ. Se denota como tan(θ) y se expresa matemáticamente de la siguiente forma:
Nuevamente, tomando como referencia la imagen en la que A y B representan las longitudes de los catetos (lados que forman el ángulo recto) y C representa la longitud de la hipotenusa, la razón trigonométrica tangente para el ángulo α queda definida de la siguiente manera:
Por otro lado, la razón trigonométrica tangente para el ángulo θ queda definida de la siguiente manera:
La tangente de un ángulo agudo también puede definirse como la razón entre el seno y el coseno del mismo ángulo. Por ejemplo, si en un triángulo rectángulo sus dos ángulos agudos se representan por α y θ, entonces la tangente del ángulo α es la razón entre el seno del ángulo α y el coseno del ángulo α. Matemáticamente, esto se expresa de la siguiente manera:
De manera similar, la tangente del ángulo θ se define como la razón entre el seno del ángulo θ y el coseno del ángulo θ. Matemáticamente, esto se expresa de la siguiente manera: