El recíproco de un número real

En matemáticas, el recíproco de un número real "a", diferente de cero, es el número que, al multiplicarse por "a", da como resultado uno.

Por ejemplo, el recíproco de 8 es 1/8 (un octavo), ya que, al multiplicar 8 por 1/8, se obtiene 1 como resultado. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}8\cdot\frac{1}{8}&=\frac{8}{1}\cdot\frac{1}{8}\\&=\frac{8\cdot 1}{1\cdot 8}\\&=\frac{8}{8}\\&=1\end{aligned}\]

El recíproco de -3 es igual a –(1/3), ya que al multiplicar -3 por -1/3 se obtiene 1 como resultado. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}-3\cdot\left(-\frac{1}{3}\right)&=\frac{-3}{1}\cdot\left(-\frac{1}{3}\right)\\&=\left(-\frac{3}{1}\right)\left(-\frac{1}{3}\right)\\&=\left(\frac{3}{1}\right)\left(\frac{1}{3}\right)\\&=\frac{3\cdot 1}{1\cdot 3}\\&=\frac{3}{3}\\&=1\end{aligned}\]

El recíproco de la fracción 5/4 (cinco cuartos) es igual a 4/5 (cuatro quintos), ya que, al multiplicar la fracción 5/4 por la fracción 4/5, se obtiene 1 como resultado. Matemáticamente, esto se expresa de la siguiente manera:

\[\begin{aligned}\frac{5}{4}\cdot\frac{4}{5}&=\frac{5\cdot 4}{4\cdot 5}\\&=\frac{20}{20}\\&=1\end{aligned}\]

A continuación, veamos la definición formal y cómo calcular el recíproco de un número real.

Tabla de contenido

Definición del recíproco de un número real
Cómo calcular el recíproco de un número real

Definición del recíproco de un número real

Dado un número real "a" diferente de cero, el recíproco de "a" es el resultado que se obtiene de dividir 1 entre "a". Si "a" es un número entero, entonces su recíproco se representa simplemente como la fracción 1/a.

Por ejemplo, el recíproco de 2 es igual a la fracción 1/2 (un medio). De manera similar, el recíproco de 7 es igual a la fracción 1/7 (un séptimo).

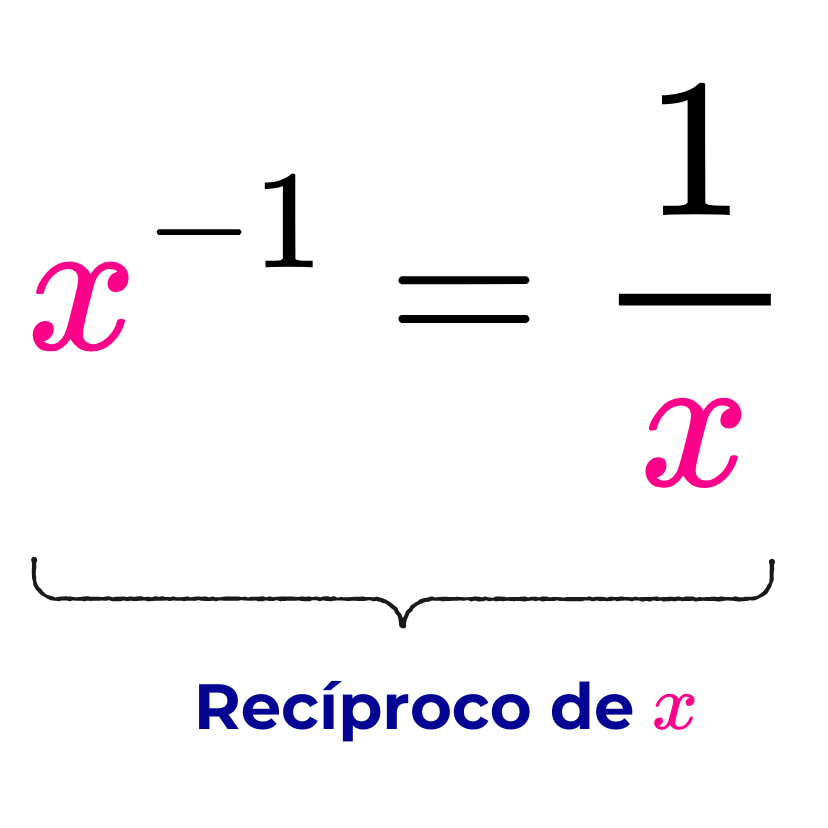
En términos de potencias, el recíproco de un número real "a", diferente de cero, puede escribirse como una potencia de base "a" con exponente negativo -1. Es decir, el recíproco de "a", además de representarse como 1/a, también puede expresarse como a^-1.

Por ejemplo, el recíproco de 2, además de escribirse como la fracción 1/2, también puede representarse como una potencia de base 2 con exponente negativo -1, es decir, el recíproco de 2 puede representarse como 2^-1.

De manera similar, el recíproco de 7 puede expresarse simplemente como una potencia de base 7 exponente -1, es decir, el recíproco de 7 puede representarse como 7^-1.

Una de las propiedades básicas del recíproco de un número real es que el producto entre un número y su recíproco siempre es igual a uno. En otras palabras, 1/a es el recíproco de "a" si su producto es igual a 1. Esta propiedad es fundamental para verificar que un número es recíproco del otro.

Al recíproco de un número real "a", diferente de cero, también se le denomina inverso multiplicativo de "a".

Cómo calcular el recíproco de un número real

En general, para calcular el recíproco de un número real "a" diferente de cero, simplemente se divide 1 entre dicho número "a".

Es importante destacar que, dado que "a" es un número real diferente de cero, este puede ser un número natural, un número entero (positivo o negativo), un número racional (fracción) o un número irracional. A continuación, veamos como calcular el recíproco de un número entero (positivo y negativo ), de un número racional, de un número irracional y de una potencia.

Para más información acerca del tema, puedes consultar el artículo "Recíproco" del sitio Disfruta las matemáticas.