Vectores: definición, tipos y características

Los vectores se clasifican según diferentes criterios, como su posición, magnitud, dirección y relación con otros vectores. Los principales tipos de vectores son los siguientes:
- Vectores unitarios
- Vectores nulos
- Vectores libres
- Vectores deslizantes
- Vectores fijos o ligados
- Vectores paralelos
- Vectores opuestos
- Vectores colineales
- Vectores coplanarios
- Vectores concurrentes o angulares
- Vectores axiales o pseudovectores
Definición de vector
Un vector es un segmento de recta orientado en un espacio vectorial. Es decir, se trata de un segmento de recta que posee magnitud, dirección y sentido. Se denota mediante una letra en negrita o con una flecha encima. Gráficamente, se representa mediante una flecha.
El término "vector" proviene del latín vector, vectoris, cuyo significado es "el que conduce" o "el que transporta".
Elementos de un vector
Los elementos que componen un vector son los siguientes:
- Módulo o magnitud: Es la longitud del vector.
- Dirección: Es la amplitud del ángulo que forma la recta que contiene al vector con respecto a la parte positiva del eje horizontal "x" en el plano cartesiano.
- Sentido: Indica la orientación del vector en un sistema de referencia. Se representa con la punta de la flecha y puede ser positivo o negativo.
- Punto de aplicación: Es el lugar desde donde actúa el vector, es decir, el punto donde inicia.
- Punto final: Es el punto donde termina el vector.
Según su magnitud, dirección, sentido y relación con otros vectores, es posible identificar distintos tipos de vectores.
Tipos de vectores según su magnitud
Vectores unitarios
Definición: Los vectores unitarios son aquellos cuya magnitud o módulo es igual a 1. Matemáticamente, si la magnitud de un vector A es igual a 1, es decir, |A|=1, entonces A es un vector unitario.
A diferencia de otros tipos de vectores que se denotan con una flecha sobre una letra, los vectores unitarios se representan con el acento circunflejo (^) sobre la letra.
Por ejemplo, los vectores unitarios asociados a las direcciones de los ejes de coordenadas cartesianas x, y, z se designan por î, ĵ y k, respectivamente.

Vector nulo
Definición: El vector nulo es aquel cuya magnitud o módulo es igual a cero. Se denota mediante la letra O en negrita o con una flecha encima.
Características:
- Todos sus componentes son iguales a cero.
- Su representación gráfica es un punto.
- Es el elemento neutro aditivo del conjunto de vectores, ya que cualquier vector sumado con el vector nulo da como resultado el mismo vector.
Tipos de vectores según su punto de aplicación
Vectores libres
Definición: Los vectores libres son aquellos cuyo punto de aplicación no está definido. Es decir, pueden trasladarse a cualquier lugar del espacio manteniendo su magnitud, dirección y sentido.
Características:
- Conservan su magnitud, dirección y sentido.
- El conjunto de todos los vectores equipolentes (vectores iguales entre sí) se denomina vector libre.
- Su punto de aplicación es libre o no está definido.
- Pueden trasladarse hacia cualquier punto del espacio sin alterar sus propiedades.

Vectores deslizantes
Definición: Los vectores deslizantes son aquellos cuyo punto inicial puede desplazarse sobre la misma recta que contiene al vector (recta de acción). En otras palabras, pueden trasladarse manteniendo su magnitud, dirección y sentido a lo largo del segmento de recta que contiene al vector.
Características:
- Mantienen su magnitud, dirección y sentido.
- Pueden deslizarse a lo largo de la recta de acción.
- El origen o punto de aplicación puede estar en cualquier punto de la recta.

Vectores fijos o ligados
Definición: Los vectores fijos son aquellos cuyo punto de aplicación es fijo. Es decir, el punto inicial del vector se encuentra en una posición específica y no puede trasladarse a otro lugar sin alterar sus propiedades.

Tipos de vectores según su dirección
Vectores paralelos
Definición: Los vectores paralelos son aquellos que tienen la misma dirección. Es decir, dos vectores son paralelos cuando los segmentos de recta que los contienen también lo son.
Características:
- El ángulo entre ellos es igual a 0° o 180°.
- Su producto cruz es igual a cero.
- Pueden tener distinto sentido y distinta magnitud.
- Sus componentes son proporcionales.

Vectores perpendiculares (ortogonales)
Definición: Los vectores perpendiculares, también llamados ortogonales, son aquellos que forman un ángulo recto. Es decir, dos vectores son ortogonales cuando el ángulo entre ellos es de 90°.
Características:
- El ángulo entre ellos es de 90°.
- Su producto punto es igual a cero.

Vectores opuestos
Definición: Los vectores opuestos son aquellos que tienen la misma magnitud y dirección, pero sentidos contrarios.
Características:
- El ángulo entre ellos es de 180°.
- Son paralelos.
- Al sumarlos, el resultado es el vector nulo.

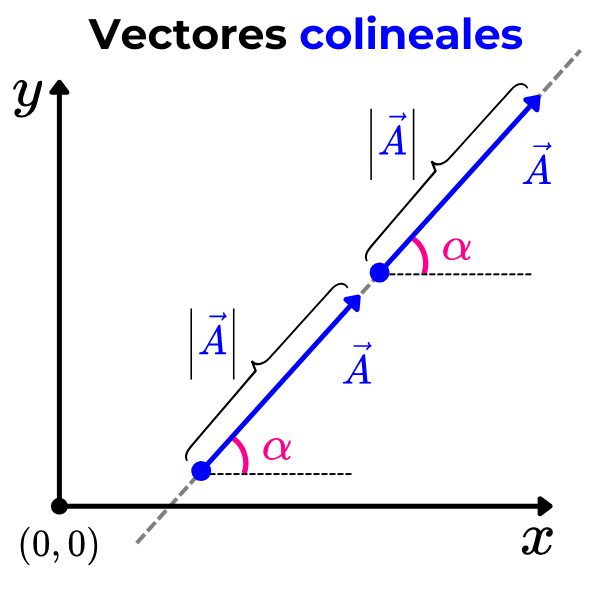
Vectores colineales
Definición: Los vectores colineales son aquellos que se encuentran sobre una misma recta o son paralelos entre sí.
Características:
- Comparten la misma línea de acción.
- Las relaciones entre sus coordenadas son iguales: (Ax/Bx)=(Ay/By)=(Az/Bz).
- El ángulo entre ellos es igual a 0° o 180°.
- Su producto cruz es igual a cero.
- Pueden tener la misma dirección, pero no necesariamente el mismo sentido.
Vectores coplanarios
Definición: Los vectores coplanarios son aquellos que se encuentran en un mismo plano. En otras palabras, las rectas sobre las que se ubican están contenidas en un mismo plano.

Otros tipos de vectores
Vectores concurrentes o angulares
Definición: Los vectores concurrentes o angulares son aquellos cuyas líneas de acción se cruzan en un mismo punto, formando un ángulo entre ellos.

Vectores axiales o pseudovectores
Definición: Los vectores axiales o pseudovectores son aquellos cuya dirección indica un eje de rotación, es decir, están asociados a efectos de giro.
- Su dirección señala un eje de rotación.
- Están relacionados con fenómenos de giro.
- Se definen mediante el producto vectorial.
- Su magnitud representa el valor numérico de la cantidad física asociada.
- Su sentido se determina mediante la regla de la mano derecha.
Vectores equipolentes
Definición: Los vectores equipolentes son aquellos que tienen la misma magnitud, dirección y sentido, aunque su punto de aplicación puede ser diferente.

Diferencia entre magnitudes vectoriales y escalares
En física, las magnitudes se clasifican en escalares y vectoriales.
Las magnitudes escalares se definen únicamente por un número real acompañado de sus unidades de medida, sin requerir dirección ni sentido.
Por otro lado, las magnitudes vectoriales no solo poseen un valor numérico y unidades de medida, sino que también están caracterizadas por una dirección y un sentido.
La elección entre una magnitud escalar o vectorial dependerá de la naturaleza de la cantidad que se mide o calcula. Por ejemplo:
- Para describir temperaturas, densidades o masas, se utilizan magnitudes escalares.
- Para representar velocidades, fuerzas, aceleraciones, momentos de torsión o campos electromagnéticos, se utilizan magnitudes vectoriales.