Triángulo rectángulo: Definición, características y tipos

Un triángulo rectángulo es un tipo de triángulo que tiene un ángulo recto, es decir, un ángulo de 90°.
En un triángulo rectángulo, los lados que forman el ángulo recto se denominan catetos, mientras que el lado opuesto a dicho ángulo se denomina hipotenusa.
- Definición de triángulo rectángulo
- Características de un triángulo rectángulo
- Tipos de triángulos rectángulos
- Teorema de Pitágoras
- Perímetro de un triángulo rectángulo
- Área de un triángulo rectángulo
- Razones trigonométricas de un triángulo rectángulo
- Propiedades de los triángulos rectángulos
- Videoclase sobre el triángulo rectángulo
- Preguntas frecuentes
Definición de triángulo rectángulo
Un triángulo rectángulo es un tipo de triángulo en el que la amplitud de uno de sus tres ángulos internos es de 90°. Los otros dos ángulos internos tienen una amplitud mayor que 0° y menor que 90°, por lo que son ángulos agudos.
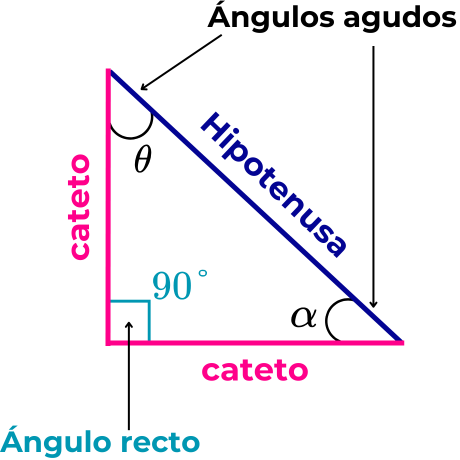
Características de un triángulo rectángulo
En un triángulo rectángulo, los lados que forman el ángulo recto se denominan catetos, y el lado opuesto al ángulo recto se denomina hipotenusa, siendo este el lado de mayor longitud comparado con las longitudes de los catetos.
Un cateto puede ser adyacente u opuesto con respecto a uno de los dos ángulos agudos del triángulo rectángulo.
Se dice que un cateto es adyacente a un ángulo agudo cuando, junto con la hipotenusa, forman a dicho ángulo agudo. Por el contrario, se considera cateto opuesto cuando, junto con la hipotenusa no forman a dicho ángulo.
Tipos de triángulos rectángulos
Los triángulos rectángulos se clasifican según la longitud de sus lados.
Según la longitud de sus tres lados, un triángulo rectángulo puede ser isósceles o escaleno.

Triángulo rectángulo isósceles
Un triángulo rectángulo isósceles es un tipo de triángulo rectángulo en el que los catetos tienen la misma longitud. Los ángulos internos, aparte del ángulo recto, son ángulos agudos y tienen la misma amplitud (45° cada uno).
Triángulo rectángulo escaleno
Un triángulo rectángulo escaleno es un tipo de triángulo rectángulo en el que los tres lados tienen diferentes longitudes. Los ángulos internos, aparte del ángulo recto, son ángulos agudos y tienen diferentes amplitudes.
Teorema de Pitágoras
El Teorema de Pitágoras relaciona las longitudes de los catetos con la longitud de la hipotenusa.
El teorema de Pitágoras establece que, en un triángulo rectángulo, la suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa. Matemáticamente, esto se expresa de la siguiente manera:
En esta fórmula, “a” y “b” corresponden a las longitudes de los catetos, mientras que “c” corresponde a la longitud de la hipotenusa.
Cuando se conocen los valores de las longitudes de los catetos “a” y “b”, la longitud de la hipotenusa “c” se puede calcular con la siguiente fórmula:
Cuando se conocen la longitud del cateto “b” y la longitud de la hipotenusa “c”, la longitud del cateto “a” se puede hallar mediante la siguiente fórmula:
Cuando se conocen la longitud del cateto “a” y la longitud de la hipotenusa “c”, se puede calcular la longitud del cateto “b” a partir de la siguiente fórmula:
Perímetro de un triángulo rectángulo
El perímetro de un triángulo rectángulo es igual a la suma de las longitudes de sus tres lados, es decir, es igual a la suma de las longitudes de los dos catetos y la longitud de la hipotenusa.
La fórmula para calcular el perímetro de un triángulo rectángulo está definida como: P=a+b+c. En esta fórmula, "a" y "b" corresponden a las longitudes de los catetos, y "c" a la longitud de la hipotenusa.
Área de un triángulo rectángulo
En un triángulo rectángulo, la altura de dicho triángulo coincide con la longitud de uno de los catetos, mientras que la base coincide con la longitud del otro cateto. De esta manera, el área de un triángulo rectángulo es igual al producto de las longitudes de los catetos dividido entre dos.
Matemáticamente, la fórmula para calcular el área de un triángulo rectángulo está definida como Área=a*b/2. En esta fórmula, "a" y "b" representan las longitudes de los catetos.
Razones trigonométricas de un triángulo rectángulo
Las razones trigonométricas de un triángulo rectángulo son las relaciones entre las longitudes de los lados y uno de sus dos ángulos agudos.
Las razones trigonométricas de un ángulo agudo en un triángulo rectángulo son el seno, el coseno y la tangente.
El seno de un ángulo agudo α es la razón entre la longitud del cateto opuesto al ángulo α y la longitud de la hipotenusa. Esta razón se expresa de la siguiente manera:
El coseno de un ángulo agudo α es la razón entre la longitud del cateto adyacente al ángulo α y la longitud de la hipotenusa. Esta razón se expresa de la siguiente manera:
La tangente de un ángulo agudo α es la razón entre la longitud del cateto opuesto y la longitud del cateto adyacente. Esta razón se expresa de la siguiente manera:
Propiedades de los triángulos rectángulos
- Tiene un ángulo interno de 90°, es decir, un ángulo recto.
- Tiene dos ángulos internos mayores a 0° y menores que 90°, es decir, dos ángulos agudos.
- Los ángulos agudos son ángulos complementarios, es decir, su suma es igual a 90°.
- La hipotenusa es el lado de mayor longitud.
- Los catetos pueden tener la misma o diferente longitud.
- El cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos.
Videoclase sobre el triángulo rectángulo
Preguntas frecuentes
Un triángulo rectángulo es un tipo de triángulo que tiene un ángulo interno de 90°.
Un triángulo rectángulo tiene un ángulo recto (90°) y dos ángulos agudos (mayores de 0° y menores de 90°). Los dos ángulos agudos son complementarios, es decir, su suma es igual a 90°.
